Question 216288: A chemist wants to mix 9 liters of 25% acid solution. Because of limited amounts on hand, the mixture is to come from three different solutions, one with 10% acid, another with 30% acid, and a third with 40% acid. The amount of the 10% solution must be twice the amount of the 40% solution, and the amount of the 30% must equal the total amount of the other two solutions. how much of each solution must be used?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A chemist wants to mix 9 liters of 25% acid solution.
Because of limited amounts on hand, the mixture is to come from three different solutions,
one with 10% acid, another with 30% acid, and a third with 40% acid.
The amount of the 10% solution must be twice the amount of the 40% solution,
and the amount of the 30% must equal the total amount of the other two solutions.
how much of each solution must be used?
:
Let x = amt of 40% solution
;
it says,"amount of the 10% solution must be twice the amount of the 40% solution"
therefore
2x = amt of 10% solution
:
it say,"amount of the 30% must equal the total amount of the other two"
therefore
3x = amt of 30% solution
:
The equation
.4x + .10(2x) + .30(3x) = .25(9)
:
.4x + .2x + .9x = 2.25
:
1.5x = 2.25
x = 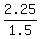
x = 1.5 liters of 40% solution
and
2(1.5) = 3 liters of 10% solution
and
3(1.5) = 4.5 liters of 30% solution
:
Check; they add up to 9 liters
and
.4(1.5) + .10(3) + .30(4.5) = .25(9)
.6 + .3 + 1.35 = 2.25
|
|
|