1. if four coins are flipped at once, what is the probability that exactly 3 tails will come up?
Two ways to do the problem, depending on what you are studying.
List the sample space:
{HHHH,HHHT,HHTH,HHTT
HTHH,HTHT,HTTH,HTTT
THHH,THHT,THTH,THTT
TTHH,TTHT,TTTH,TTTT}
Now I will color the ones red which have exactly 3 tails:
{HHHH,HHHT,HHTH,HHTT
HTHH,HTHT,HTTH,HTTT
THHH,THHT,THTH,THTT
TTHH,TTHT,TTTH,TTTT}
There are 4 out of 16, so the probabliity is  or
or  ---------------
Second way. Only use this is you are studying binomial probability.
Otherwise ignore it.
The formula for the probability of getting exactly x successes out of n
independent trials, when the probability of getting one success in one
trial is p, is
---------------
Second way. Only use this is you are studying binomial probability.
Otherwise ignore it.
The formula for the probability of getting exactly x successes out of n
independent trials, when the probability of getting one success in one
trial is p, is
 The formula for the probability of getting exactly 3 successes out of 4
independent trials, when the probability of getting one success in one
trial is
The formula for the probability of getting exactly 3 successes out of 4
independent trials, when the probability of getting one success in one
trial is  , is
, is







 ---------------------------
---------------------------
2.What is 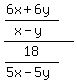
Write as a division:
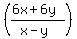 ÷
÷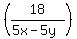 Invert the second fraction and change the division to multiplication:
Invert the second fraction and change the division to multiplication:
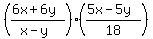 Factor
Factor  out of
out of 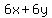 and
and  out of
out of 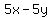
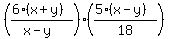 Cancel the
Cancel the  into the
into the  getting 3, and cancel the
getting 3, and cancel the 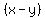 s:
s:
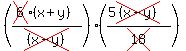

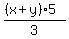
 You can either leave it like that or
distribute the top out and leave it like this:
You can either leave it like that or
distribute the top out and leave it like this:
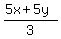 Or you can write
Or you can write  as
as 
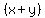
3. What is the probability of rolling two number cubes and getting the sum that is odd or a multiple of 3?
Here are all the ways a pair of fair dice (number cubes) can be rolled:
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
That is the sample space. There are 36
outcomes in that sample space.
Now I will go through and color the ones
red which are either an odd number or a
multiple of 3)
(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)
(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)
There are 24 throws out of the 36 that are either odd or are
a multiple of 3.
24 successful ways out of 36 possible ways gives a probability
of  which reduces to
which reduces to  .
Edwin
.
Edwin