Question 1203419: 12 ml of a 65% alcohol solution was mixed with 8 ml of an 80% alcohol solution. What is the concentration of the mixture?
Found 4 solutions by Edwin McCravy, josgarithmetic, ikleyn, greenestamps:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! 12 ml of a 65% alcohol solution was mixed with 8 ml of an 80% alcohol solution.
What is the concentration of the mixture?
The concentration is the percentage of alcohol in the final solution; let
that be x:
ml of solution| % expressed as a decimal| ml of pure alcohol
1st solution 12 | 0.65 | 12(0.65) = 7.8
2nd solution 8 | 0.80 | 8(0.80) = 6.4
final solution 20 | x | 14.2
20x = 14.2
x = 0.71 = 71% <--answer
Edwin
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In order to solve this problem and thousands other similar problems, a reader (a student)
should understand the method. In order for to get understanding, a reader (a student)
should hear (or read) right words describing right thoughts, at least once in his/her life,
instead of looking into tables with unknown purposes.
Solution
In this problem, there are three mixtures:
- one of 12 mL and 65% concentration;
- other of 8 mL and 80% concentration;
- third of 12+8 = 20 mL and unknown concentration.
Each concentration in this problem is the ratio of the alcohol volume to the volume of the relevant mixture.
So, to answer the problem's question, we should relate the alcohol volume in the final mixture
to the volume of the final mixture.
The volume of the final mixture is the sum of the volumes of ingredients.
The alcohol volume in the final mixture is the sum of alcohol volumes in ingredients.
12 mL of the 65% alcohol solution contribute 0.65*12 milliliters of alcohol to the final mixture.
8 mL of the 80% alcohol solution contribute 0.8*8 milliliters of alcohol to the final mixture.
So, the final mixture has 0.65*12 + 0.8*8 milliliters of alcohol from ingredients.
Therefore, we write for the final concentration
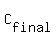 = = 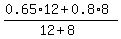 .
Having the expression, it is easy to get the number. it is .
Having the expression, it is easy to get the number. it is
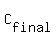 = 0.71, or 71%.
ANSWER. The final concentration is 71%. = 0.71, or 71%.
ANSWER. The final concentration is 71%.
Solved.
-------------------
Now you are armed (your mind is charged) to solve hundreds and thousands similar problems.
By knowing the general mantra, you may write your solutions in the future
in much shorter form, keeping explanations in your mind and writing the formulas only.
So, when you will get an expert level (after solving 3 - 5 similar problems),
your solution will be in one line
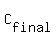 = = 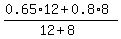 = 0.71. = 0.71.
Memorize this logic, this mantra and the structure of this formula.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is an informal method for solving this kind of 2-part mixture problem that is completely different from the standard formal algebraic methods shown by the other tutors....
The fraction of the mixture that is 80% alcohol is 8/(12+8) = 8/20 = 2/5.
That means the percentage of the mixture is 2/5 of the way from 65% to 80%.
From 65% to 80% is a difference of 15%; 2/5 of that is 6%. The percentage of the mixture is 65+6 = 71%.
ANSWER: 71%
|
|
|