Question 1203015: How many liters of water must be added to 20 liters of a 20%salt solution to make it a 12.5 % salt solution
Please i need a diagram and step by step solution.thnk you
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39701)   (Show Source): (Show Source):
Answer by greenestamps(13258)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I will show several ways to solve the problem. Since having more tools at your disposal makes you a better problem solver, I would recommend looking at and trying to understand all of them.
(1) 20% of 20 liters is 4 liters; since you are adding water (0% salt) you will still have 4 liters of salt after adding the water. 12.5% as a fraction is 1/8, so the 4 liters of salt you have must be 1/8 of the final salt solution. That means the final solution is 32 liters; and that means you added 12 liters of water.
ANSWER: 12 liters
(2) Traditional algebra...
You are mixing 20 liters of 20% salt to x liters of 0% salt to end up with (20+x) liters of 12.5% salt:




ANSWER: 12 liters
(3) Alligation (yes, with an "i") -- this method is apparently taught in pharmacology.
You asked for a diagram. This method in fact uses a diagram....
Here is the diagram for your problem:
20 12.5
12.5
0 7.5
The "20" and "0" in the first column are the percentages of salt in the two ingredients.
The "12.5" in the middle of the diagram is the percentage of the mixture.
The "12.5" and "7.5" in the third column are the differences -- calculated diagonally -- between the numbers in the first column and the number in the second column: 12.5 is the difference between 0 and 12.5, and 7.5 is the difference between 20 and 12.5.
The two numbers in the third column give you the RATIO in which the two ingredients must be mixed. In this problem, that ratio is 12.5:7.5 = 5:3. So you need 5 parts of the 20% salt solution to 3 parts of water.
Given that there are 20 liters of the 20% salt solution, find the number of liters of water using a proportion:
5:3 = 20:x
60 = 5x
x = 12
ANSWER: 12 liters
(4) Finally, here is what I think is the easiest and fastest way to solve any 2-part mixture problem like this. It is closely related to the previous method, but to me the calculations are much simpler.
You are starting with a 20% salt solution and adding 0% salt until you have a mixture that is 12.5% salt. Think of that as "starting at 20 and walking towards 0, stopping when you get to 12.5".
Mentally, or using a number line if it helps, observe/calculate that 12.5 is 3/8 of the way from 20 to 0.
That means 3/8 of the final mixture is what you are adding. (You started at 20 and walked towards 0, but you stopped when you were only 3/8 of the way there; so 3/8 of the mixture is what you are adding.)
Since 3/8 of the mixture is the water you are adding, the original 20 liters of 20% salt solution is 5/8 of the mixture.
Then, similar to the previous method, you have a proportion to solve: knowing that 5/8 of the mixture is 20 liters; you know 3/8 of the mixture which is the water you are adding is 12 liters.
ANSWER: 12 liters
Answer by ikleyn(53419)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many liters of water must be added to 20 liters of a 20%salt solution
to make it a 12.5 % salt solution
Please i need a diagram and step by step solution.thnk you
~~~~~~~~~~~~~~~~~~~~~~
It is one of standard mixture problems. Solving mixture problems and relevant teaching
(as for many other Math problems) requires not only correct manipulating with numbers.
Full/comprehensive understanding requires using correct terms, notions, conceptions, and the measurement units.
It is why I came to explain you everything related to this problem using right terminology.
The word "salt" in this problem describes either a solid substance or dry crumbly substance
like sand.
Its amount is NEVER measured in liters, which is the unit to measure fluid volumes.
In Science, technique, industry its amount is ALWAYS measured in MASS units, like grams, kilograms etc.
In this problem, where the volume of water is measured in liters, an appropriate unit
to measure an amount of salt is kilogram.
So, in this problem, all concentrations are kg/liter (kilograms per liters),
which is mass to volume unit.
The original 20% salt solution contains 20*0.2 = 4 kilograms of salt dissolved.
Since we add pure water with no salt, this amount of dissolved salt of 4 kg remains unchanged:
in the final solution we have the same mass of salt dissolved.
The final solution should be 12.5% concentration. It means that the volume V
of the final mixture must be 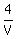 = 0.125, or V = = 0.125, or V = 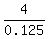 = 32 liters.
Thus, the volume of the pure water to add is this difference 32 - 20 = 12 liters.
ANSWER. 12 liters of water should be added. = 32 liters.
Thus, the volume of the pure water to add is this difference 32 - 20 = 12 liters.
ANSWER. 12 liters of water should be added.
Solved.
---------------------
The solution presented above is based on common sense (= on the mass conservation law).
For completeness purposes, I present below another solution based on simple algebra equation.
Let x be the volume of the pure water to add, in liters.
Write equation for the salt amount, which is the same in the original and final mixture
0.2*20 = 0.125*(20+x).
Left side is the dissolved salt amount in the original 20 liters of the 20% mixture.
Right side is the dissolved salt amount in the final (20+x) liters of the 12.5% mixture.
Solving this equation is easy
4 = 2.5 + 0.125x
4 - 2.5 = 0.125x
1.5 = 0.125x
x = 1.5/0.125 = 12.
You get the same answer as in the solution above: 12 liters of water should be added.
Solved in two ways, with accurate explanations.
//////////////////
To see many other similar solved problems, look into the lessons
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Special type mixture problems on DILUTION adding water
in this site.
Learn EVERYTHING related to mixture problems from these lessons.
|
|
|