You can
put this solution on YOUR website! .
A textile company has specific dyeing and drying times for its different cloths.
A roll of Cloth A requires 55 minutes of dyeing time and 45 minutes of drying time.
A roll of Cloth B requires 60 minutes of dyeing time and 30 minutes of drying time.
The production division allocates 2280 minutes of dyeing time and 1560 minutes
of drying time for the week. How many rolls of each cloth can be dyed and dried?
~~~~~~~~~~~~~~~~~
a = # of rolls Cloth A;
b = # of rolls Cloth B.
Write equations as you read the problem
55a + 60b = 2280 (1) (minutes of dyeing time)
45a + 30b = 1560 (2) (minutes of drying time)
To solve, apply the elimination method. For it, multiply equation (2) by 2 (both sides).
Keep equation (1) as is
55a + 60b = 2280 (1)
90a + 60b = 3120 (2')
From equation (2') subtract equation (1)
35a = 3120 - 2280 = 840
a = 840/35 = 24.
ANSWER. a = 24 rolls Cloth A and b =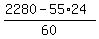 
= 16 rolls Cloth B.
Solved.
