SOLUTION: Jason forgot that his bicycle was locked up at school, so he ran to the school to get the bicycle, and then rode it back home, his running speed was 9.6kph and his riding speed was

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: Jason forgot that his bicycle was locked up at school, so he ran to the school to get the bicycle, and then rode it back home, his running speed was 9.6kph and his riding speed was      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1195535: Jason forgot that his bicycle was locked up at school, so he ran to the school to get the bicycle, and then rode it back home, his running speed was 9.6kph and his riding speed was 28.8kph, find the distance between his home and school, if the round trip took 20 minutes
Found 3 solutions by ikleyn, greenestamps, Alan3354:
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.
Jason forgot that his bicycle was locked up at school, so he ran to the school
to get the bicycle, and then rode it back home,
his running speed was 9.6kph and his riding speed was 28.8kph,
ind the distance between his home and school, if the round trip took 20 minutes
~~~~~~~~~~~~~~ 

Let d be the distance to the school.

Write time equatoin

    d%2F9.6 + d%2F28.8 = 1%2F3  of an hour (which is 20 minutes).


Multiply both sides by 3*9.6*28.8.  You will get

    3*28.8d + 3*9.6d = 9.6*28.8


Simplify and find d

        115.2d       = 276.48

             d       = 276.48/115.2 = 2.4 kilometers.    ANSWER

Solved.



Answer by greenestamps(13200) About Me  (Show Source):
You can put this solution on YOUR website!


Observe that his riding speed of 28.8km/hr is exactly 3 times his running speed of 9.6km/hr. Since the distances to and from school are the same, he spent 3 times as long running as riding.

Then, since the total time was 20 minutes, he spent 15 minutes (1/4 hour) running and 5 minutes (1/12 hour) riding.

So the distance between his home and school is (1/4)(9.6) = 2.4km, or (1/12)(28.8) = 2.4km.

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
Jason forgot that his bicycle was locked up at school, so he ran to the school to get the bicycle, and then rode it back home, his running speed was 9.6kph and his riding speed was 28.8kph, find the distance between his home and school, if the round trip took 20 minutes
--------------------
The average speed of the round-trip is 2*9.6*28.8/(9.6+28.8) = 19.2*28.8/38.4
= 14.4 km/hr
---------
d = r*t = 14.4*(1/3) = 4.8 km RT
= 2.4 km each way
------------------------------
The formula for average speed of a round-trip, or 2 trips of equal length, is:
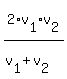
2%2Av%5B1%5D%2Av%5B2%5D%2F%28v%5B1%5D%2Bv%5B2%5D%29
It's similar to parallel resistance, parallel work, etc., just the factor of 2 is different.
There are too many formulas for any human to remember them all, but this one is easy.