Question 1183433: A manufacturer has found that if his product is priced at N90/unit then his weekly demand is 50 units, but the demand rises to 60 units per week if the selling price is N70/unit. His weekly fixed cost is N3, 000 and variable cost N20/unit.
Find the level of production which maximizes profit and determine the maximum profit?
Answer by ikleyn(52777)   (Show Source):
You can put this solution on YOUR website! .
A manufacturer has found that if his product is priced at N90/unit then his weekly demand is 50 units,
but the demand rises to 60 units per week if the selling price is N70/unit. His weekly fixed cost is N3, 000
and variable cost N20/unit. Find the level of production which maximizes profit and determine the maximum profit?
~~~~~~~~~~~~~~~~~~
Let "n" be the number of units produced and sold.
Then the total cost function is C(n) = 3000 + 20n.
Now we want to determine the revenue function, and for it, we need to know the unit selling price as the function of production.
The problem tells us that the unit selling price falls N20 from N90 to N70 when production rises 10 units from 50 to 60.
We assume (as always in such problems), that the unit selling price function p(n) is linear, so it is p(n) = 90 - 2(n-50).
Therefore, the revenue is
R(n) = n*p(n) = n*(90-2(n-50)) = 90n -2n^2 + 100n = -2n^ + 190n.
Now the profit is
P(n) = R(n) - C(n) = -2n^2 + 190n - 3000 - 20n = -2n^2 + 170n - 3000. (1)
The problem asks about the maximum of the profit, which is the vertex of the quadratic function (1).
The maximum happens at n = "  ", which is 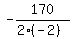 =  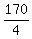= 42.5.
The number of units must be integer, so the solution are two integer numbers closest to 42.5, i.e. 42 and 43.
To find the maximum profit, substitute this found value n= 42 into the profit function (1)
P(42) = -2*42^2 + 170*42 - 3000 = 612.
ANSWER. The optimal production level is of 42 or 43 units generating the maximum profit of N612.
The plot to provide visual check.
Plot R(n) = -2n^2 + 170n - 3000 (red) and the plot y = 612 (green)
Solved.
|
|
|
