Question 1182966: An oil refinery refines types 1 and 2 of crude oil and can refine as much as 4000 barrels each week. Type 1 crude has 2 kg of impurities per barrel, type 2 has 3 kg of impurities per barrel,and the refinery can handle no more than 9000 kg of these impurities each week.How much of each type should be refined in order to maximize profits, if the profit is R25/barrel for type 1 and R30/barrel for type 2?
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! x = number of barrels of type 1
y = number of barrels of type 2
your constraints are:
x + y <= 4000
2x + 3y <= 9000
your would graph the opposite of these inequalities in the desmos.com calculator.
the unshaded area is your region of feasibility.
the maximum profit is at the corners of the region of feasibility.
your graph looks like this:
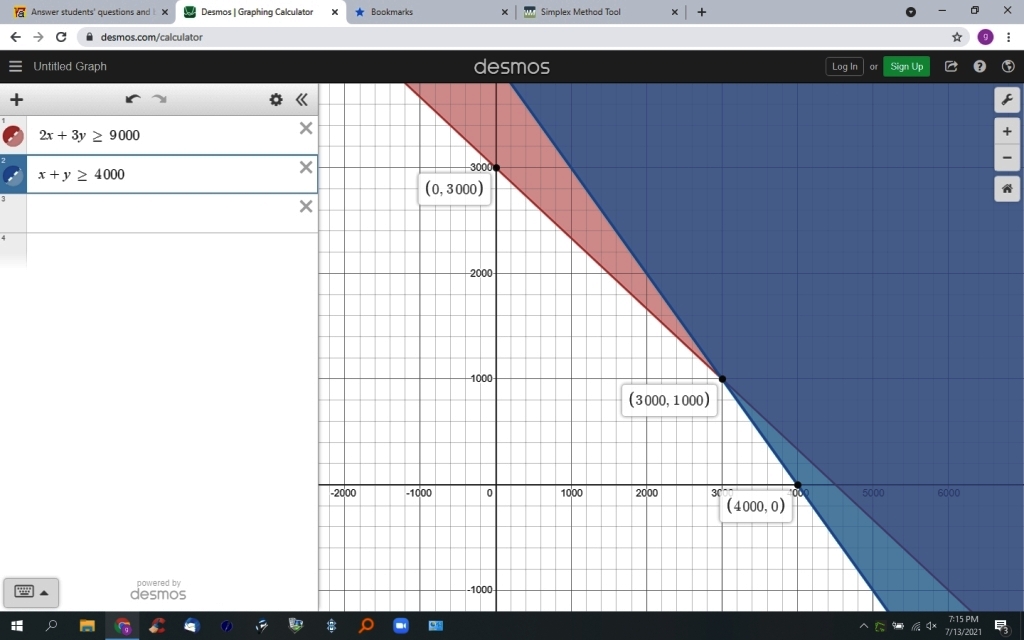
your corner points are (x,y) = (0,3000), (3000,1000), (4000,0)
your objective function is 25x + 30y.
this is what you want to maximize.
you evalute the objective function at each of your corner points.
(0,3000) = 0 * 25 + 3000 * 30 = 90,000
(3000,1000) = 3000 * 25 + 1000 * 30 = 105,000
(4000,0) = 4000 * 25 + 0 * 30 = 100,000
your maximum profit is when you refine 3000 barrels of type 1 and 1000 barrels of type 2.
all your constraints need to be satisfied.
at your maximum point of (3000,1000), .....
x + y = 4000 <= 4000
2x + 3y = 2 * 3000 + 3 * 1000 = 6000 + 3000 = 9000 <= 9000
all your constraints are satisfied at your maximum profit point.
all looks good.
your solution is that 3000 barrels of type 1 and 1000 barrels of type 2 need to be refined for maximum profit.
Answer by greenestamps(13219)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The solution from the other tutor is fine.
However, there is a refinement of the process he shows that cuts down a bit on the amount of work you need to do to finish the problem.
Every resource you will find on linear programming says that, after finding the corners of the feasibility region, you have to evaluate the objective function at all the corners to find the maximum value of the objective function.
That is not true.
The corner where the objective function is maximized can be determined by comparing the slope of the objective function to the slopes of the constraint boundary lines.
In this problem, we have, for the equations of the constraint boundary lines,
x+y = 4000 ==> y = -x+4000 ==> slope -1
2x+3y = 9000 ==> y = (-2/3)x+3000 ==> slope -2/3
For the objective function, we have
25x+30y = C ==> y = (-5/6)x+C/30 ==> slope -5/6
Since the slope of the objective function is between the slopes of the two constraint boundary lines, the maximum value of the objective function will be at the intersection of the two constraint boundary lines.
It can be seen that this is the case by looking at the graph. Of all the lines with slope -5/6, the one which "first touches" the feasibility region will be the one that touches the corner of the feasibility region that is the corner where the two lines that intersect at that corner have slopes for which the slopes of the two lines are one greater than and one less than -5/6.
So to find the maximum value of the objective function, you only need to evaluate it at (3000,1000)
|
|
|