Question 1180854: You need a 95% alcohol solution. On hand, you have a 15 mL of a 10% alcohol mixture. How much pure alcohol will you need to add to obtain the desired solution?
You will need
(?) mL of pure alcohol
to obtain
(?) mL of the desired 95% solution.
Found 5 solutions by josgarithmetic, math_tutor2020, MathTherapy, ikleyn, greenestamps:
Answer by josgarithmetic(39617)   (Show Source):
Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!
The question is
"How much pure alcohol will you need to add to obtain the desired solution?"
So we'll make that x and the goal of course is to find x.
x = amount of pure alcohol to add to the existing mix
The existing solution is 15 mL of 10% alcohol
Meaning, 15*0.10 = 1.5 mL of pure alcohol is present in this bottle.
So x+1.5 mL of pure alcohol is the total after adding those x mL of pure alcohol.
The total amount of solution is x+15 mL (which consists of pure alcohol plus water).
The ratio
(x+1.5)/(x+15)
represents the percentage of alcohol after we add in that x mL of pure alcohol.
Set this ratio equal to 0.95 and solve for x
(x+1.5)/(x+15) = 0.95
x+1.5 = 0.95(x+15)
x+1.5 = 0.95x+14.25
x-0.95x = 14.25-1.5
0.05x = 12.75
x = 12.75/0.05
x = 255
If we add 255 mL of pure alcohol to the original 1.5 mL of pure alcohol, then we have 255+1.5 = 256.5 mL of pure alcohol.
The total amount of solution is x+15 = 255+15 = 270 mL
Note how
256.5/270 = 0.95 = 95%
showing we have a 95% alcohol mix now.
--------------------------------------
Answers:
You'll need to add 255 mL of pure alcohol
This will lead to 270 mL of 95% solution
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
You need a 95% alcohol solution. On hand, you have a 15 mL of a 10% alcohol mixture. How much pure alcohol will you need to add to obtain the desired solution?
You will need
(?) mL of pure alcohol
to obtain
(?) mL of the desired 95% solution.
Let amount of pure alcohol, be A
Then we get: .1(15) + A = .95(15 + A)
.1(15) + A = .95(15) + .95A
A - .95A = .95(15) - .1(15)
.05A = .85(15)
Amount of pure alcohol to mix, or 
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
You need a 95% alcohol solution. On hand, you have a 15 mL of a 10% alcohol mixture.
How much pure alcohol will you need to add to obtain the desired solution?
~~~~~~~~~~~~~~~
Some people proudly solve such problems MENTALLY, without using any equation.
They construct their REASONING this way . . .
The given starting mixture contains 0.1*15 mL = 1.5 mL of the pure alcohol.
The rest 15 mL - 1.5 mL = 13.5 mL is water.
Now, we are going to add pure alcohol - so we do not change the mass of water, those 13.5 mL.
These 13.5 mL are going to become 5% = 100% - 95% of the final mixture.
Hence, the volume of the final mixture must be 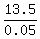 = 270 mL.
It means that the volume of the pure alcohol to add is 270 mL - 15 mL = 255 mL.
ANSWER. 255 mL of pure alcohol should be added, and the final volume of the mixture will be 270 mL.
Solved.
It is how COMMON SENSE helps to solve problems without using any equations.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is another very fast way to solve this kind of problem mentally....
You are mixing 10% alcohol with 100% alcohol to get a mixture of 95% alcohol.
95% is 85/90 = 17/18 of the way from 10% to 100%. (Picture the three percentages 10, 95, and 100 on a number line, if it helps. From 10 to 95 is a difference of 85; from 10 to 100 is a difference of 90; 85/90 = 17/18.)
That means 17/18 of the mixture has to be the 100% alcohol, which means 1/18 of the mixture is the 15mL of 10% alcohol.
So the amount of 100% alcohol is 17*15mL = 255mL.
ANSWER: 255mL
|
|
|
