Question 1178938: How much of Brand A fruit punch (55%
fruit juice) must be mixed with 2 L of
Brand B fruit punch (40% fruit juice) to
create a mixture containing 50% fruit
juice?
Found 4 solutions by mananth, josgarithmetic, ikleyn, greenestamps:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website! percent ---------------- quantity
Brand B 40 ---------------- 2 l
Brand A 55 ---------------- x l
Mixture 50 ---------------- 2 + x l
0.4 * 2 + 0.55 x = 0.5 ( 2 + x)
0.8 + 0.55 x= 1 + 0.5 x
0.05 x= 1 - 0.8
0.05 x= 0.2 -
x= 4 liters Brand A
Answer by josgarithmetic(39617)  (Show Source):
Answer by ikleyn(52787)  (Show Source):
You can put this solution on YOUR website! .
When people come to the forum with such problems, they should learn THE LOGIC of the solution,
and that is all what they should know.
The people should not know these formulas, that @josgarithmetic tries to sell you.
Even do not try to understand or memorize these formulas --- keeping them in your mind is absolutely useless
and will teach you to NOTHING.
THEREFORE, for a sake of your safety, ignore his post and do not load this TRASH into your head / (mind).
May god saves you from it . . .
Keep your mind clean for more useful/vital tasks of your life.
Also, keep in mind that @josgarithmetic is one of "quasi-" and "pseudo-" tutors
at this forum, producing nonsensical "solutions", unsuitable for teaching and for learning.
/\/\/\/\/\/
@josgarithmetic, every time, as I see similar "solution"
from you at this forum, I will issue this message to a visitor.
@josgarithmetic, I promised it to you long time ago to react in this way
to such your posts, and you know it - - - so now I fulfill my promise . . .
///////////
Below is the solution presented in the form as it SHOULD BE done to learn from it . . .
Let x be the amount of Brand A (the volume in liters) to be mixed.
It contains 0.55x liters of the pure juice.
2 liters of the Brand B contain 0.4*2 liters of the pure juice.
So, ingredients contain 0.55x + 0.4*2 liters of the pure juice.
The resulting mixture has the volume of (x + 2) liters and contains 0.5*(x+2) liters of the pure juice.
So we make the equation
0.55x + 0.4*2 = 0.5*(x+2), (1)
saying that amount of the pure juice in ingredients is the same as in the final mixture.
From this equation
x = 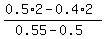 = 4 liters.
ANSWER. 4 liters of the Brand A must be mixed.
CHECK. I will check if equation (1) is valid.
Its left side is 0.55*4 + 0.4*2 = 3 liters of the pure juice.
Its right side is 0.5*(4+2) = 3 liters.
We have true equality - so the solution is correct.
Solved, answered and explained. And completed.
---------------
It is a standard and typical mixture problem.
For introductory lessons covering various types of mixture word problems see
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
(1) Certainly memorizing a magic formula as shown by tutor @josgarithmetic is not a good way to LEARN HOW to work problems like this.
(2) Formal algebraic solutions as shown by the other tutors -- in which it is clear WHY the method works -- are of course fine.
(3) And if a formal algebraic solution is not required, here is what is almost certainly the fastest and easiest path to the answer.
Consider, perhaps using a number line, that the 50% of the mixture is 2/3 of the way from 40% to 55%, the percentages of the two ingredients.
That means 2/3 of the mixture must be the 55% ingredient.
So the 2L of the 40% juice is 1/3 of the mixture; that means the 2/3 of the mixture that is the 55% juice is 4L.
ANSWER: 4L of 55% juice.
CHECK:
.4(2)+.55(4) = .8+2.2 = 3
.5(6) = 3
|
|
|
