Question 1178068: A chemist needs 8 liters of a 25% acid solution. The solution is to be mixed from three solutions whose concentrations are 10%, 20%, and 50%. How many liters of each solution will satisfy each condition?
a. Use as little as possible of the 50% solution
b. Use as much as possible of the 50% solution.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A chemist needs 8 liters of a 25% acid solution. The solution is to be mixed from three solutions
whose concentrations are 10%, 20%, and 50%. How many liters of each solution will satisfy each condition?
a. Use as little as possible of the 50% solution
b. Use as much as possible of the 50% solution.
~~~~~~~~~~~~~~
(a) It is intuitively clear that if you want to use as little as possible of the 50% solution,
you should not use 10% solution at all, and should use the 20% solution, mixing it with the 50% solution.
In this case, let x liters be the amount of the 50% solution to use
and let (8-x) liters be the amount of the 20% to add.
Then you have this equation for the pure acid volume
0.5x + 0.2*(8-x) = 0.25*8
From the equation, x =  = =  = 1 = 1  .
ANSWER. 1 .
ANSWER. 1  liters of the 50% acid solution and the rest, 6 liters of the 50% acid solution and the rest, 6  liters of the 20% acid solution.
(b) It is intuitively clear that if you want to use as much as possible of the 50% solution,
you should not use 20% solution at all, and should use the 10% solution, mixing it with the 50% solution.
In this case, let x liters be the amount of the 50% solution to use
and let (8-x) liters be the amount of the 10% to add.
Then you have this equation for the pure acid volume
0.5x + 0.1*(8-x) = 0.25*8
From the equation, x = liters of the 20% acid solution.
(b) It is intuitively clear that if you want to use as much as possible of the 50% solution,
you should not use 20% solution at all, and should use the 10% solution, mixing it with the 50% solution.
In this case, let x liters be the amount of the 50% solution to use
and let (8-x) liters be the amount of the 10% to add.
Then you have this equation for the pure acid volume
0.5x + 0.1*(8-x) = 0.25*8
From the equation, x =  = = 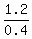 = 3.
ANSWER. 3 liters of the 50% acid solution and the rest, 5 liters of the 10% acid solution. = 3.
ANSWER. 3 liters of the 50% acid solution and the rest, 5 liters of the 10% acid solution.
Solved.
|
|
|