Question 1172204: Eric wishes to mix together some common stone worth $0.10 per kilogram and some granite chips worth $0.15 per kilogram to produce a decorative garden mixture. How much of each stone should be mixed to obtain 300 kg of a mixture worth $0.13 per kilogram?
Found 3 solutions by ikleyn, josgarithmetic, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Let x be the amount of the material worth $0.15 per kilogram. (I even do not want to use its long name)
Then the amount of the other material is (300-x) kilograms.
Now you write the total money equation
0.15x + 0.1*(300-x) = 0.13*300.
Left side is the total cost of ingredients, while the right side is the cost of the final mixture.
From the equation, you get
x = 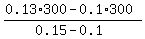 = 180.
ANSWER. 180 kg of the decorative garden mixture and the rest material, 300-180 = 120 kg is the common stone.
Solved.
----------------
It is a standard and typical mixture problem.
In this site, there is entire bunch of lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for dry substances like coffee beans, nuts, cashew and peanuts
- Word problems on mixtures for dry substances like candies, dried fruits
- Word problems on mixtures for dry substances like soil and sand
- Word problems on mixtures for alloys
- OVERVIEW of lessons on word problems for mixtures
A convenient place to quickly observe these lessons from a "bird flight height" (a top view) is the last lesson in the list.
Read them and become an expert in solution the mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
/\/\/\/\/\/\/\/\/
I want to add my thoughts about the @josgarithmetic solution.
When a visitor comes to this forum with such problem, it is naturally to assume that this person is a beginner
and does not know how to solve it.
Typically, it is a young student of 6th -7th grade.
Such students practically NEVER worked with symbolic equations; and, typically, they DO NOT UNDERSTAND them, at all.
In middle school, the teachers NEVER teach students solving such problems using symbolic equations.
THEREFORE, I insistently recommend all visitors to ignore this and similar posts by @josgarithmetic.
Answer by josgarithmetic(39617)  (Show Source):
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @josgarithmetic likes that formula with all those variables for solving mixture problems like this.
If you use that method to solve mixture problems, you won't learn anything about problem solving. Plugging numbers into a formula doesn't really teach you anything.
Tutor @ikleyn shows a standard algebraic method for solving the problem. If you pay attention to how the method works, you will learn something useful about problem solving using formal algebra.
But if a quick and easy solution without formal algebra is acceptable, here is the fastest way to solve this, or any similar mixture problem.
(1) The price per kg of the mixture $0,13, is 3/5 of the way from $0.10 to $0.15. (If you don't see that, picture the three numbers 0.10, 0.13, and 0.15 on a number line....)
(2) That means 3/5 of the mixture is the more expensive ingredient.
ANSWER: 3/5 of 300kg, or 180kg, of the more expensive granite chips; the other 120kg is the common stone.
CHECK:
180(0.15)+120(0.10) 27+12 = 39
300(0.13) = 39
|
|
|
