Question 1156558: How many gallons of 20% alcohol solution and 50% alcohol solution must be mixed to get 9 gallons of 30% alcohol solution?
Found 4 solutions by josgarithmetic, ikleyn, greenestamps, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source):
Answer by ikleyn(52782)  (Show Source):
You can put this solution on YOUR website! .
Let x be the amount of the 20% alcohol solution (in gallons),
and y be the amount of the 50% alcohol solution.
Your first equation is
x + y = 9 (1)
for the total volume.
There are 0.2x gallons of the pure alcohol in the x gallons of the 20% solution,
and there are 0.5y gallons of the pure alcohol in the y gallons of the 50% solution.
So, there are, in total, 0.2x + 0.5y gallons of the pure alsohol in ingredients.
It should be equal to the amount of the the pure alcohol in the mixture, 0.3*9.
It gives you the second equation
0.2x + 0.5y = 0.3*9 gallons (2)
Thus you have the system of two equations, (1) and (2).
From equation (1), express x = 9-y and substitute it into the second equation, replacing x You will get
0.2*(9-y) + 0.5y = 2.7.
From this equation
y = 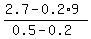 = 3.
So, the problem is just solved.
ANSWER. 3 gallons of the 50% solution, and the rest, (9-3) = 6 gallons of the 20% solution.
CHECK. I will calculate the concentration of the mixture. It is 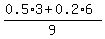 = 0.3 = 30%. ! Precisely correct !
Solved.
-----------------
It is a standard and typical mixture problem.
For introductory lessons covering various types of mixture word problems see
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn solves the problem by the traditional algebraic method, using two equations and two unknowns. This is a good example of how to use algebra to solve problems; you should understand it.
Tutor @josgarithmetic shows how to solve the problem using his/her favorite formula for solving mixture problems, involving a whole bunch of variables. If you like to memorize ugly formulas (generally without understanding WHERE those formulas come from) then you can use that method.
But if a formal algebraic solution is not required, here is a way you can solve the problem mentally in a few seconds:
(1) 30% is "twice as close to 20% as it is to 50%". (to help you see this, picture the three percentages 20, 30, and 50 on a number line....)
(2) Therefore, the mixture must contain twice as much of the 20% alcohol as it does the 50% alcohol.
9 gallons total, with twice as much 20% alcohol as 50% alcohol means 6 gallons of 20% and 3 gallons of 50%.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website!
How many gallons of 20% alcohol solution and 50% alcohol solution must be mixed to get 9 gallons of 30% alcohol solution?
Let amount of 20% solution be T
Then amount of 50% solution = 9 - T
We then get the following: .2T + .5(9 - T) = .3(9)
.2T + 4.5 - .5T = 2.7
.2T - .5T = 2.7 - 4.5
- .3T = - 1.8
Amount of 20% solution, or 
You should now be able to find the amount of 50% solution to mix!
|
|
|
