.
All these questions relate to Calculus.
(a) The particle is instantaneously in rest when its velocity is equal to zero
v = 0, i.e. 9 - t^2 = 0.
It means t^2 = 9, t = 
= 3 seconds. ANSWER
(b) The position (the current coordinate) is ANTI-DERIVATIVE of the speed, i.e.
position x = 
= 9t - 
.
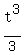The particle is again at its starting point when its position is zero
position x = 0, or 9t - 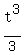= 0, or 27*t- t^3 = 0, t*(27-t^2) = 0,
t =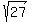 
= 
seconds = 5.196 second (approx.) ANSWER
The speed at this moment is the value of v = 9 - t^2 at t = , i.e.
v = 9 -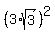 
= 9 - 9*3 = 9 - 27 = -18 meters per second.
(c) Total distance is the sum of distances traveled "to there" and "back".
The returning point is the point where the velocity becomes equal to zero.
We just found, that the time to get this point is t = 3 seconds (see part a) above).
The distance traveled "to there", is [ 9t - 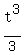] at t= 3 seconds, or 9*3 - 
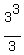= 27 - 
= 27 - 9 = 18 meters.
So, one way distance is 18 meters; hence, two-ways distance is 2*18 = 36 meters. ANSWER
The plot below illustrates the movement.
The plot shows the position of the body (y-coordinate) as the function of the time (x-coordinate).
The body started from the point (0,0).
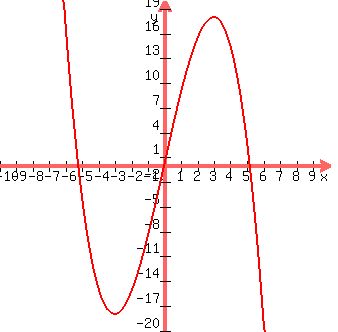Plot y = the position coordinate 9t - .
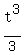Solved. // All questions are answered.
