Question 1154197: A chemical company makes two brands of antifreeze. The first brand is 45% pure antifreeze, and the second brand is 85% pure antifreeze. In order to obtain 40 gallons of a mixture that contains 75% pure antifreeze, how many gallons of each brand of antifreeze must be used?
Found 4 solutions by josmiceli, MathTherapy, greenestamps, ikleyn:
Answer by josmiceli(19441)   (Show Source): (Show Source):
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A chemical company makes two brands of antifreeze. The first brand is 45% pure antifreeze, and the second brand is 85% pure antifreeze. In order to obtain 40 gallons of a mixture that contains 75% pure antifreeze, how many gallons of each brand of antifreeze must be used?
.45F + .85(40 - F) = .75(40)
.45F + 34 - .85F = 30
- .4F = - 4
F, or 

Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The quickest way to the answer to a mixture problem like this involving two ingredients:
75% is three-fourths of the way from 45% to 85%.
Therefore, three-fourths of the mixture is the higher percentage ingredient.
ANSWER: 3/4 of 40 gallons, or 30 gallons, of 85% antifreeze, the other 10 gallons of 45% antifreeze.
Answer by ikleyn(52921)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Antifreeze is a mixture of water with some liquid chemical - ethylene glycole or propylene glycole.
For purposes of this problem, you don't need know exactly, what these chemicals are.
It is quite enough to know that antifreeze is a mixture of water with some liquid chemical.
In school math, there are two major approaches/ways to solve such problems.
In my post, I will show you one of them --- using two-equations setup.
Let x be the volume of the first brand (in gallons), and y be the volume of the second brand.
Then the total volume of the mixture is (x+y) gallons.
First brand contains 45% of the antifreeze, which is 0.45x gallons of pure antifreeze.
Second brand contains 85% of the antifreeze, which is 0.85x gallons of pure antifreeze.
Therefore, from the condition, you have these two equations
x + y = 40 gallons (1)
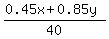 = 0.75 gallons (2)
First equation is for the total volume of the mixtures.
In second equation, the numerator is the volume of the pure antifreeze.
Divided by the denominator (40 gallons), it is the concentration of the resulting mixture, which is given as 75%,
by the condition.
Thus (1) and (2) are two basic equations to solve the problem.
Taken together, they form the setup for the given problem. They are the base to solve the given problem.
This setup is called "2-equations setup".
If you understand, how these equations are constructed, why they have their form, then you just understand the problem.
Now our task is to solve the system of equations.
To do it, first multiply both sides of the equation (2) by 40. You will get then this system
x + y = 40 (3)
0.45x + 0.85y = 0.75*40 (4)
Next, from equation (3), express x = 40-y and substitute it into equation (4). You will get
0.45*(40-y) + 0.85*y = 0.75*40
-0.45y + 0.85y = 0.75*40 - 0.45*40
y = = 0.75 gallons (2)
First equation is for the total volume of the mixtures.
In second equation, the numerator is the volume of the pure antifreeze.
Divided by the denominator (40 gallons), it is the concentration of the resulting mixture, which is given as 75%,
by the condition.
Thus (1) and (2) are two basic equations to solve the problem.
Taken together, they form the setup for the given problem. They are the base to solve the given problem.
This setup is called "2-equations setup".
If you understand, how these equations are constructed, why they have their form, then you just understand the problem.
Now our task is to solve the system of equations.
To do it, first multiply both sides of the equation (2) by 40. You will get then this system
x + y = 40 (3)
0.45x + 0.85y = 0.75*40 (4)
Next, from equation (3), express x = 40-y and substitute it into equation (4). You will get
0.45*(40-y) + 0.85*y = 0.75*40
-0.45y + 0.85y = 0.75*40 - 0.45*40
y = 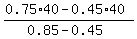 = 30.
So, 30 gallons of the second brand should be used.
Then it is clear (or derive it from equation (1)) that the volume of the first brand should be 40-30 = 10 gallons.
ANSWER. 10 gallons of the first brand and 30 gallons of the second brand.
CHECK. There is no need to check equation (1), since right now we derived the first brand volume from it.
In reality, we should check equation (2) only : = 30.
So, 30 gallons of the second brand should be used.
Then it is clear (or derive it from equation (1)) that the volume of the first brand should be 40-30 = 10 gallons.
ANSWER. 10 gallons of the first brand and 30 gallons of the second brand.
CHECK. There is no need to check equation (1), since right now we derived the first brand volume from it.
In reality, we should check equation (2) only : 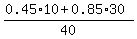 = 0.75 = 75%. ! Precisely correct ! = 0.75 = 75%. ! Precisely correct !
The problem is just solved.
--------------------
As an after-solution conclusion, I want to make a notice.
In the solution process, I did not make each single calculation separately.
I created the final formula, and then used Excel in my computer.
I don't know, which calculation tool do you have: pocket calculator or some software on your comp.
I don't know which calculation tool you are assigned to use.
But I used to deduce all my calcs to one formula (when possible); then I copy the formula into a cell in Excel
spreadsheet and get the answer in one click (and with no errors). Again: in one click with no errors (!)
You may perform differently - I prefer do not submerge in these details.
Same way I make my check: I write formula, then copy and paste it into Excel cell and then get an answer in one click.
Therefore, all talks if it is economic solution path from the calculation point of view or not - are out me:
it is not my goal to discuss it with the student at this level / (at this stage).
At this stage, my goal is to teach on how to solve the problem by Algebra methods.
Now, what I wrote above, is appropriate to teach the student, when he or she solves the problem first time in his or her life.
When the student will solve such problems 2-3 times, he (or she) will be inclined to write the solution in much shorter way.
Now I want to present you this short way.
Let x be the volume of the first brand (in gallons), and y be the volume of the second brand.
Then from the condition, you have these two equations
x + y = 40 gallons (1) (total volume equation)
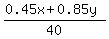 = 0.75 (2) (the concentration equation)
You can write equation (2) in the form
0.45x + 0.85y = 0.75*40
Next, from equation (3), express x = 40-y and substitute it into equation (4). You will get
0.45*(40-y) + 0.85*y = 0.75*40
From this equation, express y and calculate
y = = 0.75 (2) (the concentration equation)
You can write equation (2) in the form
0.45x + 0.85y = 0.75*40
Next, from equation (3), express x = 40-y and substitute it into equation (4). You will get
0.45*(40-y) + 0.85*y = 0.75*40
From this equation, express y and calculate
y = 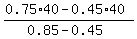 = 30.
So, 30 gallons of the second brand should be mixed with 40-30 = 10 gallons of the first brand. ANSWER
CHECK. We should check equation (2) only : = 30.
So, 30 gallons of the second brand should be mixed with 40-30 = 10 gallons of the first brand. ANSWER
CHECK. We should check equation (2) only : 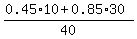 = 0.75 = 75%. ! Precisely correct ! = 0.75 = 75%. ! Precisely correct !
It is the short form solution.
There is the shortest form, too, when all explanations are omitted, as follows:
x + y = 40 gallons (total volume equation)
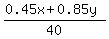 = 0.75 (the concentration equation)
0.45x + 0.85y = 0.75*40
0.45*(40-y) + 0.85*y = 0.75*40
y = = 0.75 (the concentration equation)
0.45x + 0.85y = 0.75*40
0.45*(40-y) + 0.85*y = 0.75*40
y = 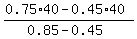 = 30.
So, 30 gallons of the second brand should be mixed with 40-30 = 10 gallons of the first brand. ANSWER
CHECK. = 30.
So, 30 gallons of the second brand should be mixed with 40-30 = 10 gallons of the first brand. ANSWER
CHECK. 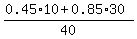 = 0.75 = 75%. ! Precisely correct ! = 0.75 = 75%. ! Precisely correct !
So, only 7 lines are required for the solution, including one line for the answer and 1 line for the check -- when you know the method.
Interesting, that there is even shorter way, when you use ONE-EQUATION setup.
Then two lines are totally enough to place your solution.
But since my post is already too long, I can tell you about it next time, if you ask me about it.
Or, alternatively, you may learn it from the links that follow.
--------------------
It is a standard and typical mixture problem.
There is entire bunch of lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions (*)
- Word problems on mixtures for dry substances like coffee beans, nuts, cashew and peanuts
- Word problems on mixtures for dry substances like candies, dried fruits
- Word problems on mixtures for dry substances like soil and sand
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
- Advanced mixture problems
- Advanced mixture problem for three alloys
- Unusual word problem on mixtures
- Check if you know the basics of mixtures from Science
- OVERVIEW of lessons on word problems for mixtures
in this site.
Among them, the lesson marked (*) in the list is specially devoted to antifreeze mixtures.
A convenient place to quickly observe these lessons from a "bird flight height" (a top view) is the last lesson in the list.
Read them and become an expert in solution the mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|