SOLUTION: A 10% salt solution is to be mixed with pure water to produce 45 gallons of a 3% salt solution. How much of each are needed?

The first and the major step in solving such problems is to understand what is a 10% salt solution  and what is a 3% salt solution.


The concentration in such problems is measured in kilograms of salt per liter of the mixture.


A 10% salt solution is 1 liter of water with dissolved 100 grams of salt in it - or any proportional mixture.    (1)


A 3% salt solution is 1 liter of water with dissolved 30 grams of salt in it - or any proportional mixture.      (2)



    These are not unique possible definitions.

    One can define a 10% salt solution as a mixture that contains 10% of salt by weight (by total mass of the solution).

    It is not exactly the same definition as (1) - these two definitions are slightly different.

    But in school Math, students and teachers usually NEGLECT this difference,
    and consider and accept (1) and (2) as the basic definitions.


So, taking into account that 1 gallon = 3.785 liters, we can say that 45 gallons of 3% salt solution contain

      45*3.785*0.03 kilograms of salt.    (3)


Since we obtained these 45 gallons of the 3% salt solution by adding water,
our original 10% salt solution contained exactly this (= the same) amount (3) of salt.


Hence, the volume of the original 10% salt solution was 

     volume = 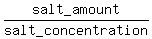 =  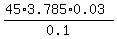= 45*3.785*0.3 liters.


It means that the volume of water added is the difference

    volume of water added = 45*3.785 - 45*3.785*0.3 liters = 45*3.785*(1-0.3) = 45*3.785*0.7 liters.    (4)



If you want to express this volume in gallons, you must divide (4) by the conversion factor of 3.785.


Thus the volume of water to add in gallons is  45*0.7 = 31.5 gallons.    ANSWER