Question 1144968: The average of three unequal positive whole numbers is 10. What is the largest possible value that any of those numbers can have ?
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! The average of three unequal positive whole numbers is 10. What is the largest possible value that any of those numbers can have ?
---------
If zero (0) is considered, it's 20.
If not, it's 19.
Answer by ikleyn(52781)  (Show Source):
You can put this solution on YOUR website! .
The largest possible value, under the given conditions, is 27.
It is achieved for THIS set of integer positive numbers {1, 2, 27}.
ANSWER. The largest possible value that any of those numbers can have is 27.
To get the answer, it is clear, that the two other numbers must be as small as it is possible, under the condition.
Thinking in this way, you immediately obtain the equation
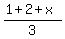 = 10
from which you immediately obtain the solution x = 27.
|
|
|
