Question 1143737: If | x-2 | >0, which of the following cannot be true?
A)x>2y
B)x<2y
C) x=2y
D)x=17
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website! If | x-2 | >0, which of the following cannot be true?
A)x>2y
B)x<2y
C)x=2y
D)x=17
Let's pick some values for x and y for each choice and see
which one cannot be true.
Let's try choice A:
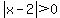 , , 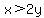 Let's pick x=1 and y=0.4
Let's pick x=1 and y=0.4
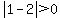 , , 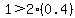
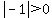 , , 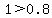
 , , 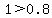 Both those are true, so answer A can be true, so A is not the
correct choice.
--------------------------------------
So let's try choice B:
Both those are true, so answer A can be true, so A is not the
correct choice.
--------------------------------------
So let's try choice B:
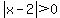 , , 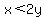 Let's pick x=1 and y=1
Let's pick x=1 and y=1
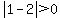 , , 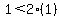
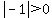 , , 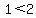
 , , 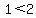 Both those are true, so answer B can be true, so B is not the
correct choice.
--------------------------------------
So let's try choice C:
Both those are true, so answer B can be true, so B is not the
correct choice.
--------------------------------------
So let's try choice C:
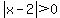 , ,  Let's pick x=4 and y=2
Let's pick x=4 and y=2
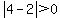 , , 
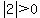 , , 
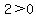 , ,  Both those are true, so answer C can be true, so C is not the
correct choice.
--------------------------------------
So let's try choice D:
Both those are true, so answer C can be true, so C is not the
correct choice.
--------------------------------------
So let's try choice D:
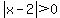 , ,  We must pick x=17
We must pick x=17
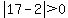 , , 
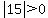 , , 
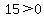 , ,  Both those are true, so answer D can be true, so D is not the
correct choice.
--------------------------------------
So either you copied the problem wrong, or the teacher gave you a
botched problem.
Edwin
Both those are true, so answer D can be true, so D is not the
correct choice.
--------------------------------------
So either you copied the problem wrong, or the teacher gave you a
botched problem.
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers A, B, and C are nonsense, because the problem says nothing about what "y" is. So none of them can be the answer.
And ANSWER D is true.
So the problem is faulty as shown.
|
|
|