Question 1143632: A rectangle is drawn on a coordinate plane. I have the coordinates of one corner of the rectangle is (0,-5) and the coordinates of the opposite corner is (7,3), Then what is the area of the rectangle
A)-21
B)21
C)56
D)105
Answer by ikleyn(52782)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Actually, you are given only one diagonal of a rectangle as a segment in a coordinate plane.
It is NOT ENOUGH to determine the area of a rectangle.
It is not enough to restore THE rectangle by an UNIQUE way as a shape.
Think about this (such) rectangle as inscribed to the circle.
You are given only the diameter of this circle as the segment in the plane,
but you can have INFINITELY MANY rectangles inscribed to this circle.
By the way, the length of the diagonal is 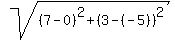 = = 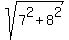 = = 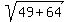 = = 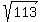 .
The maximum possible area of such a rectangle is .
The maximum possible area of such a rectangle is 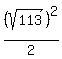 = = 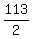 = 56.5 square units,
when a rectangle becomes a square with the given diagonal length.
So, the answer can not be A), since the area can not be negative.
The answer can not be D), too, since it is TOO BIG value (= impossible value).
But the answer CAB BE B) or C), and you CAN NOT distinct between these two cases. = 56.5 square units,
when a rectangle becomes a square with the given diagonal length.
So, the answer can not be A), since the area can not be negative.
The answer can not be D), too, since it is TOO BIG value (= impossible value).
But the answer CAB BE B) or C), and you CAN NOT distinct between these two cases.
Answered, explained, solved and completed.
|
|
|