Question 1138792: A mixture of 12% disinfectant solution is to be made from 10% and 18% disinfectant solutions. How much of each solution should be used if
32 gallons of the 12% solution are needed?
There needs to be __ gallons of 10% solution and __ gallons of 18% solution.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
0.18x + 0.10*(32-x) = 0.12*32
x = 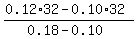 = 8.
ANSWER. 8 gallons of the 18% solution and the rest, 32-8 = 24 gallons of the 10% solution.
CHECK.  = 0.12 = 12% final concentration. ! Correct !
-----------------
It is a standard and typical mixture problem.
For introductory lessons covering various types of mixture word problems see
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Typical word problems on mixtures from the archive
in this site.
You will find there ALL TYPICAL mixture problems with different methods of solutions,
explained at different levels of detalization, from very detailed to very short.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
Answer by greenestamps(13200)  (Show Source):
You can put this solution on YOUR website!
Here is a completely different way of solving mixture problems like this. If you understand it, it will get you to the solution to this kind of problem much faster and with far less work than the traditional algebraic method.
(1) Determine, as a fraction, how far the target percentage is from one given percentage to the other: 12% is 1/4 of the way from 10% to 18%. (From 10 to 18 is 8; from 10 to 12 is 2; 2/8 = 1/4.)
(2) That means 1/4 of the mixture has to be the 18% solution.
Then, since a total of 32 gallons of the 12% solution is needed, the amount of 18% solution is 1/4 of 32 = 8 gallons; the other 24 gallons are the 10% solution.
------------------------------
NOTE to tutor @ikleyn....
At the time I saw your response, there was a typo in the last line showing the amounts of the two ingredients....
|
|
|
