Question 1110573: Brine containing 4 lbs/gal of salt enters a large tank at the rate of 4 gal/min and the solution well-stirred leaves at 2 gal/min. The tank initially contains 30 gal of water. • Set up an equation determining the amount of salt in the tank at any time t in minutes. • What is the amount of salt in the tank after 10 minutes? • When will there be 170 lbs of salt in the tank?
Found 2 solutions by addingup, KMST:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! the salt enters the tank at rate:
R_in = (4gal/min)(4lbs/gal) = 16lbs/min
Since the tank loses liquid at a rate of 2gal/min:
4gal/min - 2gal/min = 2gal/min
after t minutes the number of gallons of brine in the tank is:
30 + 2t gallons
after 10 minutes:
30 + 2(10) = 50 gallons
and
50(4) = 200lbs of salt
----------------------------------
170/4 = 42.5gallons of brine
42.5-30 = 12.5 gallons of brine need to be added
12.5/2 = 6.25 minutes to get 170lbs of salt in the tank
--------------------------------------------
I think this is what you were looking for.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! My best attempted estimate is that after 10 minutes the tank would contain
a total of  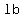 of salt (in a total of 50 gallons of solution). of salt (in a total of 50 gallons of solution).
I reached that estimate through a computational approach, described below.
The situation is complicated,
because as brine with a fixed 4 lb/gallon concentration is entering the tank,
dilute salt solution of varying concentration is continuously leaving the tank.
That makes me think that the problem would require solving complicated differential equations.
It also requires ignoring chemistry inconsistencies, and considering negligible
all differences between the final volume of a mix of solutions and the sum of the volumes mixed.
Ignoring all practical aspect flaws in the design of this problem,
the concentration of salt in the tank would approach 4 lb/gallon over time,
but it would reach exactly that value at    . .
As the solution is "well stirred", the concentration of salt in the tank, and in the solution leaving the tank would be increasing over time.
We can simplify the problem by ignoring some of the salt losses to get a slight overestimate of the amount of salt in the tank.
During the first 0.5 minutes, volume has increased by 1 gallon (2 gallons in, 1 gallon out).
So after 0.5 minutes, the volume is 31 gallons.
In the 2 gallons of brine that entered the tank, 8 lb of salt came in.
As the solution is "well stirred", the concentration of salt in the tank,
and the amount of salt leaving the tank during the first 0.5 minutes is not exactly zero.
to simplify the problem, we can say that it was about  . .
Then, we can say that at  the concentration of salt in the tank is the concentration of salt in the tank is
 . .
To continue simplifying, let's say that the concentration in the stream leaving the tank
is that same 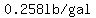 for the next 0.5 minutes. for the next 0.5 minutes.
Then at  , having gained another , having gained another  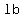 of salt, of salt,
and having lost  of salt, of salt,
the tank contains  of salt. of salt.
At the same time, the volume is 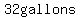 , so at , so at 
the concentration in the tank is  . .
If we keep simplifying the calculation by saying that
the  is the concentration in the stream leaving the tank for the next 0.5 minutes, is the concentration in the stream leaving the tank for the next 0.5 minutes,
by  the tank has the tank has
gained another  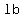 of salt, of salt,
and lost 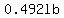 of salt. of salt.
So, at  minutes the tank contains minutes the tank contains
 of salt, of salt,
in a total of 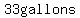 of solution, of solution,
with a concentration of  . .
Continuing with this simplified calculation, we get 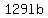 of salt at of salt at  . .
That is an overestimate, because we are underestimating the loss of salt duringt every 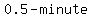 interval. interval.
Reducing the calculation intervals, increases accuracy (and calculation work).
Using a similar calculation with shorter 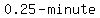 intervals intervals
yields 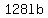 of salt in the tank after 10 minutes. of salt in the tank after 10 minutes.
That is also slight overestimate, but good enough.
NOTES:
I do not know what the person(s) who proposed the problem expect(s),
but the situation is nowhere as simple as they expect.
A problem similar to this one may appear in a chemical engineering course.
The concentration flowing into the tank would be less, as 4 lb/US gallon (and even 4 lb/Imperial gallon) exceeds the solubility of salt in water.
The students would know that as you mix solutions the weights of solution and salt add up,
but the volumes do not exactly add up, so they would use data tables
showing density of solutions as function of concentration and temperature,
and of course, the temperatures of the tank contents and stream flowing into the tank would be stated in the problem.
|
|
|