SOLUTION: a and b working together can do a given job in 4 days, b and c together can do the job in 3 days and a and c together can do it in 2.4 days. In how many days can each do the job wo

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: a and b working together can do a given job in 4 days, b and c together can do the job in 3 days and a and c together can do it in 2.4 days. In how many days can each do the job wo      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1097081: a and b working together can do a given job in 4 days, b and c together can do the job in 3 days and a and c together can do it in 2.4 days. In how many days can each do the job working alone.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
Rates a, b, c in JOBS per DAY

system%28a%2Bb=1%2F4%2Cb%2Bc=1%2F3%2Ca%2Bc=1%2F2.4%29

-

system%284a%2B4b=1%2C3b%2B3c=1%2C24a%2B24c=10%29

system%284a%2B4b=1%2C3b%2B3c=1%2C12a%2B12c=5%29
Try to use the first two of these equations to eliminate b. You'll get an equation in variables a and c, and use this with the last equation 12a%2B12c=5.

Answer by ikleyn(52782) About Me  (Show Source):
You can put this solution on YOUR website!
Let "a", "b" and "c" be the rate-of-work of each of the persons A, B, and C respectively.

We are given that 

a + b = 1%2F4,      (1)
b + c = 1%2F3,      (2)
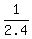a + c = 1%2F2.4.    (3)

To solve the system (1), (2), (3), let us start adding the equations (1), (2) and (3).
You will get 

2a + 2b + 2c = 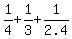1%2F4+%2B+1%2F3+%2B+1%2F2.4 = 6%2F24+%2B+8%2F24+%2B+10%2F24 = %286%2B8%2B10%29%2F24 = 1.

Hence, 

a + b + c = 1/2.    (4)

Thus we just found the combined rate-of-work of the three persons working together. It is 1%2F2 of job per day.


Now we have to find individual rate-of-work for each person. For it, let us first subtract the equation (1) from (4). You will get

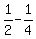c = 1%2F2+-+1%2F4 = 1%2F4.


Next, subtract the equation (2) from (4). You will get

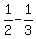a = 1%2F2+-+1%2F3 = 1%2F6.


Finally, subract the equation (3) from (4). You will get

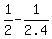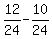b = 1%2F2+-+1%2F2.4 = 12%2F24+-+10%2F24 = 2%2F24 = 1%2F12.


Answer. The individual rates of work are 1%2F4 for C, 1%2F6 for A and 1%2F12 for B (in job-per-day units).

        So,  A will complete the job in 6 days;  B will complete the job in 12 days;  and C will complete the job in 4 days.


For many other similar solved problems See the lesson
    - Joint-work problems for 3 participants
in this site.


Also,  you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this textbook under the topic
"Rate of work and joint work problems"  of the section  "Word problems".


Save the link to this online textbook together with its description

Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson

to your archive and use it when it is needed.


================
Notice.  The way on how I solved the system of equations is  THE  STANDARD  WAY  of dealing with such special systems.


The way that @gosgarithmetic proposes in his solution is the way to  NOWHERE.