Question 1094062: How many gallons of a fruit drink that is 50% real juice must be mixed with a fruit drink that is 20% real juice to obtain 12 gallons of a fruit drink that is 40% real juice?
I have attempted to make a chart as follows, but I'm not sure I have the numbers in the correct spots. Ignore the lines in between numbers, that's just to separate the different parts of the chart.
x | .50 | .50x
12 | .40 | .40(12)
x+12 | .20 | .20(x+12)
Found 4 solutions by greenestamps, josgarithmetic, MathTherapy, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You're on the right track; but some of the expressions in your chart don't match the given information.
In your chart, the last amount is supposed to be the number of gallons in the final mixture. The problem says you are making 12 gallons of mixture, so that number should be 12. Your chart shows "12+x" in that location.
So if x is the first amount in the first column of your chart, and 12 is to be the last amount in the first column, then what must the second expression in your first column be? That is, what algebraic expression, when added to "x", gives an answer of "12"?
Of course, when you get the expressions in the first column fixed, it will cause changes elsewhere in your chart. But then you will be ready to write and solve the equation that leads to the answer.
This is the part of setting up a problem like this that most students stumble over. You will see this kind of thing many times in algebra. Get it figured out for this problem and you will be ready when you see this kind of thing again.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! You could make a chart or table if you want.
Without a table of data,
x, volume of the 50% juice
12-x, volume of the 20% juice
12 gallons of 40% juice is wanted.

OR

Solve for x and evaluate 12-x.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! How many gallons of a fruit drink that is 50% real juice must be mixed with a fruit drink that is 20% real juice to obtain 12 gallons of a fruit drink that is 40% real juice?
I have attempted to make a chart as follows, but I'm not sure I have the numbers in the correct spots. Ignore the lines in between numbers, that's just to separate the different parts of the chart.
x | .50 | .50x
12 | .40 | .40(12)
x+12 | .20 | .20(x+12)
With x being the amount of 50% real juice, the amount of 20% real juice will be 12 - x, since the total in the final mixture is 12 gallons. We then get:
x | .50 | .50x
12 - x | .20 | .20(12 - x)
12 | .40 | .40(12)
Do you see now how it should be set up?
You then use the 3rd column: .5x + .2(12 - x) = .4(12) to solve.
Solve that for x, the amount of 50% real juice and you should get 8 gallons.
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
How many gallons of a fruit drink that is 50% real juice must be mixed with a fruit drink that is 20% real juice
to obtain 12 gallons of a fruit drink that is 40% real juice?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "x" be the volume (in gallons) of the 50% real juice, which is under the question.
Then the volume of the 20% of the fruit juice to mix is 12-x gallons.
The volume of the pure juice in x gallons of 50% real juice is 0.5x gallons.
The volume of the pure juice in (12-x) gallons of 20% real juice is 0.2*(12-x)) gallons.
The total volume of the pure juice in the mix is the sum of these amounts, i.e.
0.5x + 0.2*(12-x) gallons.
The concentration of pure juice in the mixture is this fraction 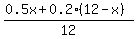 .
According to the condition, it must be equal to 40%, or 0.4.
It gives you an equation .
According to the condition, it must be equal to 40%, or 0.4.
It gives you an equation
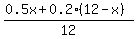 = 0.4.
It is your governing equation to find x.
To solve it, multiply both sides by 12. You will get
0.5x + 0.2*(12-x) = 0.4*12,
0.5x + 2.4 - 0.2x = 4.8,
0.5x - 0.2x = 4.8 - 2.4,
0.3x = 2.4 ====> x = = 0.4.
It is your governing equation to find x.
To solve it, multiply both sides by 12. You will get
0.5x + 0.2*(12-x) = 0.4*12,
0.5x + 2.4 - 0.2x = 4.8,
0.5x - 0.2x = 4.8 - 2.4,
0.3x = 2.4 ====> x = 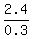 = =  = 8.
Answer. You need to use 8 gallons of 50% real juice and (12-8) = 4 gallons of 20% real juice.
Check. 8*0.5 + 4*0.2 = 4.8. 12*0.4 = 4.8. ! Correct ! = 8.
Answer. You need to use 8 gallons of 50% real juice and (12-8) = 4 gallons of 20% real juice.
Check. 8*0.5 + 4*0.2 = 4.8. 12*0.4 = 4.8. ! Correct !
Solved.
I prefer do not use the tables at all when solving such problems.
Simple logic leads you step by step along the solution from the beginning to the end, if you do know and understand this logic.
Making table only distract you from the solution.
But I do not insist that my way is the only applicable.
I think that the tables play the role of crutches.
If you do understand the logic, you do not need tables.
And working to understand the logic is your goal.
The way to it is practice.
---------------------
There is entire bunch of introductory lessons covering various types of mixture problems
- Mixture problems
- More Mixture problems
- Solving typical word problems on mixtures for solutions
- Word problems on mixtures for antifreeze solutions
- Word problems on mixtures for alloys
- Typical word problems on mixtures from the archive
in this site.
Read them and become an expert in solution mixture word problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook in the section "Word problems" under the topic "Mixture problems".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
=================
By the way, writing by @gosgarithmetic is I N C O R R E C T.
|
|
|