Question 1091513: DF Appliances has assembly plants in Atlanta and Fort Worth, where they produce a variety of kitchen appliances, including a 12-cup coffee maker and a cappuccino machine. At the Atlanta plant, 160 of the 12-cup models and 200 of the cappuccino machines can be assembled each hour. At the Fort Worth plant, 800 of the 12-cup models and 200 of the cappuccino machines can be assembled each hour. CDF Appliances expects orders for at least 64 000 of the 12-cup models and at least 40 000 of the cappuccino machines. At each plant, the number of assembly hours available for these two appliances is constrained by each plantís capacity and the need to fill the orders. Let x be the number of assembly hours at the Atlanta plant, and let y be the number of assembly hours at the Fort Worth plant. For CDF appliances to meet the expected orders, what is the minimum number of hours that needs to be allocated at each manufacturing plant? (Tip: Solve the system of inequalities and identify the extreme
point(s) of the region of solution).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your objective function is x + y which is what you want to minimize.
x equals the total assembly hours at atlanta and y equals the total assembly hours at fort worth.
your constraint functions are:
160x + 800y >= 64000
200x + 200y >= 40000
160x represents the number of 12 cup coffee makers that can be assembled in x hours at atlanta.
800y represents the number of 12 cup coffee makes that can be assembled in y hours at fort worth.
200x represents the number of cappucino machines that can be assembled in the same x hours at atlanta.
200y represents the number of cappucino makers that can be assembled in the same y hours at fort worth.
for example:
if the number of assembly hours at atlanta was 5 hours and the number of assembly hours was 10 hours at fort worth, then:
5 * 160 and 10 * 800 = 8800 12 cup coffee makers assembled at both plants.
in summary:
objective function is x + y which is what you want to minimize.
constraint functions are:
160x + 800y >= 64000
200x + 200y >= 40000
using the decmos.com calculator, you would graph the opposite of the inequalities and your feasible region would be the area of the graph that is not shaded.
the corner points of the graph will tell you the minimum number of total hours that you would require after you evaluated the objective function at each of those corner points.
here's the graph.
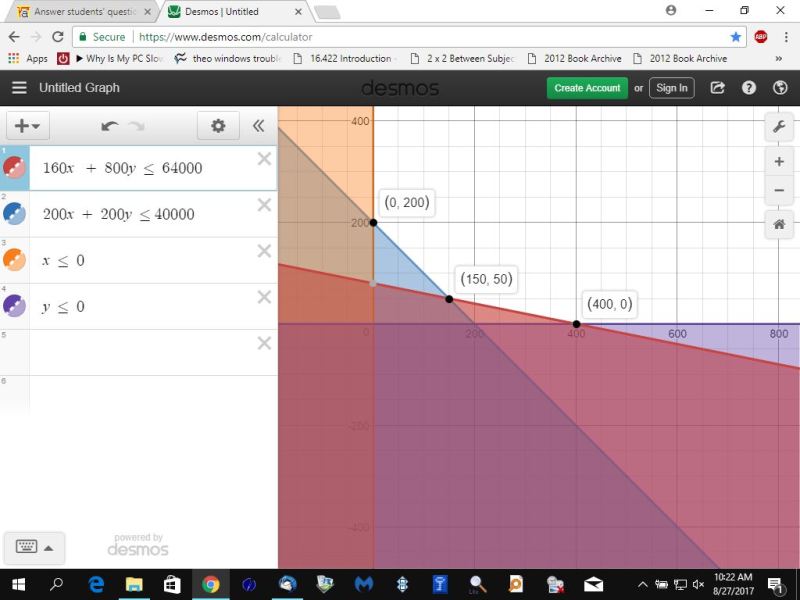
the corner points in (x,y) format are evaluated with the objective function of x + y.
(0,200) yields a total number of hours of 200.
(150,50) yields a total number of hours at 200.
(400,0) yields a total number of hours at 400.
all the constraints have to be satisfied at each of the corner points, or they would be disqualified from consideration.
with (0,200, we get 200 * 800 coffee makers and 200 * 200 cappucino machines.
that'a a total of 160,000 coffee makers and a total of 40,000 cappucino machines, therefore satisfying the constraints and then some.
with (150,50), the number for each plant are:
atlanta makes 150 * 160 coffee makers and 50 * 200 cappucino machines.
fort worth makes 50 * 800 coffee makers and 50 * 200 cappucino machines.
that'a a total of 64,000 coffee makers and a total of 40,000 cappucino machines, therefore satisfying the constraints.
(400,0) is out of consideration because the total hours are more than the other options.
so you have a tie between (0,200) and (150,50).
however, (150,50) satisfies the requirements exactly without making an excess of 12 cup cofee makers.
since the total cost of production is assembly hours plus material plus finishing hours plus testing hours plus packaging hours, then it makes sense to take (150,50) as the solution as that would minimize the cost as well.
furthermore, if you only require about 64,000 coffee makers and you make 160,000, then you will have a lot of them sitting around and not being sold for quite a while, thereby increasing your inventory expense as well as spending money that you could have used for something else.
this gets into more complex considerations than it appears that you were asked.
the simple answer is a tie between (0,200) and (150,50).
|
|
|