Question 1078955: One canned juice drink is 25% orange juice; another is 5% orange juice. How man liters of each should be mixed together in order to get 20L that is 21% orange juice?
How many liters of the 25% orange juice should me in the mixture?
Found 3 solutions by stanbon, jorel1380, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! One canned juice drink is 25% orange juice; another is 5% orange juice. How man liters of each should be mixed together in order to get 20L that is 21% orange juice?
How many liters of the 25% orange juice should me in the mixture?
------
orange + orange = orange
0.25x + 0.05(20-x) = 0.21*20
---------------------------
25x + 5*20 - 5x = 21*20
-----
20x = 16*20
x = 16L (amt. of 25% mix to use)
---------
Cheers,
Stan H.
------------
Answer by jorel1380(3719)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let n and 20-n be the amounts of 25% o.j. and 5% o.j., respectively. Then
.25n+0.05(20-n)=0.21(20)
0.2n+1=4.2
0.2n=3.2
n=16
You need 16L of 25% juice, and 4L of 5% juice. ☺☺☺☺
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the amount (the volume, in liters) of the 25% orange juice to mix.
Then the required volume of the 5% orange juice is (20-x) liters.
The amount of the pure orange juice in the mixture is
0.25x + 0.05(20-x)
(motice that 0.25 is 25% and 0.05 is 5%).
This amount of the orange juice must be equal to 0.21*20 = 4.2 liters, as the condition requires.
So, you get this equation
0.25x + 0.05*(20-x) = 4.2.
Simplify and solve for x:
0.25x + 1.0 - 0.05x = 4.2,
0.2x = 4.2 - 1.0,
0.2x = 3.2
x = 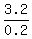 = 16.
Answer. 16 liters of the 25% juice and 20-16 = 4 liters of the 5% juice must be mixed.
Check. 0.25*16 + 0.05*4 = 4 + 0.2 = 4.2 liters of the pure juice.
Then the percentage of the pure juice in 20 liters of liquid is = 16.
Answer. 16 liters of the 25% juice and 20-16 = 4 liters of the 5% juice must be mixed.
Check. 0.25*16 + 0.05*4 = 4 + 0.2 = 4.2 liters of the pure juice.
Then the percentage of the pure juice in 20 liters of liquid is 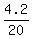 = 0.21 = 21%. Correct !! = 0.21 = 21%. Correct !!
|
|
|