SOLUTION: How many gallons of a 10% acid solution must be mixed with 5 gal of a 30% acid solution to make a 14% acid solution?

Let "x" be a required amount of the 10% acid solution, in gallons.

Then the 10% solution contains 0.1*x gallons of the pure acid.
     The 5 gallons of 30% acid solution contains 0.3*5 gallons of the pure acid.
After mixing, the new solution contains 0.1x + 0.3*5 of the pure acid, while the total volume of the solution is (5+x) gallons.

The equation for concentration of the new solution is

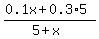 = 0.14.

To solve it, multiply both sides by (5+x). You will get

0.1x + 1.5 = 0.14*(5+x),  or

0.1x + 1.5 = 0.7 + 0.14x,  or

1.5 - 0.7 = 0.14x - 0.1x,  or

0.8 = 0.04x.

Hence,  x = 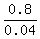 = 20 gallons.

Answer.  20 gallons of the 10% acid solution must be added.