Question 1045922: Zaina is curios about numbers that contain the number 2,0,1,6 in that exact sequence she insists that the digits 2,0,1,6 only occur once in the numbers. She calls such a number a "year number". for example 20163 and 320164 are year numbers but 12016 and 21069 are not year numbers. Find the 2016th Year number.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Luckily we are in the 2010's, and luckier yet, Zaina wants the digits 2, 0, 1, and 6 to appear only once. That makes it easier.
It is easier to think through than to explain, but I will try.
The first year number is, of course 2016. That is  year number. year number.
Next come the 5-digit numbers that we can make by adding one of the remaining 6 digits (3, 4, 5, 7, 8, and 9) to the back of 2016. That is  more. more.
Then come the 5-digit numbers that we can make by adding one of the remaining 6 digits to the front of 2016.
That is another  numbers, for a total of numbers, for a total of  5-digit year numbers. 5-digit year numbers.
After that, we have 6-digit year numbers formed by adding a 2-digit sequence to 2016.
There are  2-digit sequences that can be formed with the digits 3, 4, 5, 7, 8, and 9, 2-digit sequences that can be formed with the digits 3, 4, 5, 7, 8, and 9,
and there are  ways to add them to 2016. We can attach the last 2, 1, or 0 of the digits in a sequence to the back of 2016, and put the remainder of the sequence at the front. ways to add them to 2016. We can attach the last 2, 1, or 0 of the digits in a sequence to the back of 2016, and put the remainder of the sequence at the front.
That gives us  6-digit year numbers. 6-digit year numbers.
We can also make 7-digit year numbers that will be larger than all the 6-digit year numbers.
We make them by adding to 2016 3-digit sequences made from the digits 3, 4, 5, 7, 8, and 9.
There are  such sequences, from 333 to 999, such sequences, from 333 to 999,
and we can add them by including he first 0, 1, 2, or 3 digits to the front of 2016, and the rest of the sequence to the back of 2016.
That is  ways, and gives us ways, and gives us  7-digit year numbers. 7-digit year numbers.
So far, we have  year numbers with 7 digits or less. year numbers with 7 digits or less.
The largest of those is 9992016,which is The 985th year number.
There are a lot of 8-digit year numbers, and among those will be the 2016th year number.
To get to the 2016th year number, we just need to form the smallest  8-digit year numbers. 8-digit year numbers.
We make 8-digit year numbers by adding a 4-digit sequence to 2016.
With the 6 digits 3, 4, 5, 7, 8, and 9, we can make  such sequences, such sequences,
from 3333 to 9999.
The  8-digit year numbers by adding a 4-digit sequence to 2016 8-digit year numbers by adding a 4-digit sequence to 2016
formed by adding all digits in those 4-digit sequences to the back of 2016,
20163333 to 20169999 are the smallest.
The 8-digit year numbers formed by including one or more digits from those 4-digit sequences at the front 2016 start at 32016333, which is larger than 20169999.
The question now is which of the 4 digit sequences from 3333 to 9999 is the 1031st.
If we count the first 8-digit year number, 20163333, as our element 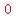 , ,
we are looking for element 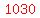 . .
In a base 6 system, using only the 6 characters 0, 1, 2, 3, 4, and 5.
the base 10 number 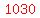 is written as is written as  , ,
because  . .
We cannot use the digits 2, 0, 1, or 6, so we would use.
 instead of instead of  , ,
 instead of instead of  , ,
 instead of instead of  , ,
 instead of instead of  , ,
 instead of instead of 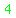 , and , and
 instead of instead of  . .
The first 8-digit year number, our element number 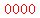 in our usual base 10 system, in our usual base 10 system,
is element number 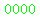 in the base 6 system using the digits in the base 6 system using the digits  to to  , ,
and is element 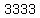 in base 6 when our characters are 3, 4, 5, 7, 8, and 9, and those are the last 4 digits of the first 8-digit year number. in base 6 when our characters are 3, 4, 5, 7, 8, and 9, and those are the last 4 digits of the first 8-digit year number.
The 1031st 8-digit year number, our element number 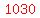 in a base 10 numbering system, in a base 10 numbering system,
element number  in a base 6 numbering system using the digits in a base 6 numbering system using the digits  to to  , ,
is written as 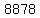 in base 6 when our characters are 3, 4, 5, 7, 8, and 9. in base 6 when our characters are 3, 4, 5, 7, 8, and 9.
Those are the last 4 digits of the 1031st 8-digit year number.
So, the 2016th year number is formed by adding 8878 to the back of 2016.
The 2016th year number is 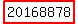 . .
|
|
|