Question 1034619: Hi, the pharmacist gives me a 1.5 liter bottle of 20% solution and asks me to mix with water to make as much 12% solution as possible. How much water will I use?
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
Hi, the pharmacist gives me a 1.5 liter bottle of 20% solution and asks me to mix with water to make as much 12% solution as possible.
How much water will I use?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the volume of water to add, in liters.
Then the volume of the new solution is 1.5 + x liters.
The original 1.5 liters of solution contains 1.5*0.2 liters of the pure substrate (remember, 0.2 = 20%).
So, you have this equation to find x:
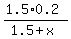 = 0.12,
where 0.12 is the concentration of the new solution.
To solve it, multiply both sides by (1.5+x), and you will get
0.3x = 1.5*0.12 + 0.12x,
0.3x - 0.12x = 0.18,
0.18x = 0.18,
x = 1.
Answer. 1 liter of water should be added.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! you have 1.5 liters of a liquid that contains 20% solution.
the amount of solution in the liquid is equal to .2 * 1.5 = .3 liters of solution.
you want to add enough liquid to make a 12% solution.
the new solution will have x liters of liquid.
your formula becomes .3/x = .12
this formula says that .3 liters of solution divided by x liters of liquid = a ratio of .12 which is equal to 12%.
solve for x to get x = .3/.12 = 2.5 liters.
your new 12% solution will be 2.5 liters.
since the original 20% solution has 1.5 liters, you added 1 liter of liquid.
you could also have solved this as follows:
you have 20% solution in 1.5 liters of liquid.
the number of liters of solution is equal to .2 * 1.5 = .3 liters of solution.
you want to add x liters of 0% solution to this to get a new solution that is 12% solution.
this new solution will contain 1.5 + x liters of liquid.
your formula becomes:
.2 * 1.5 + .0 * x = .12 * (1.5 + x)
simplify this equation to get .3 = .18 + .12 * x
subtract .18 from both sides of this equation to get .12 = .12 * x
divide both sides of this equation by .12 to get .12/.12 = x
solve for x to get x = 1.
you get the same answer either way.
you add 1 liter of 0% solution to 1.5 liters of 20% solution to get 2.5 liters of 12% solution.
in this problem, water is the 0% solution that you added.
|
|
|
