Question 1034450: One alloy is 2 parts iron to 3 parts silver and another alloy is 7 parts iron to 3 parts silver. How much of each should be combined to produce a 30 pound alloy that is 1 part iron to 1 part silver?
Found 2 solutions by jorel555, ikleyn:
Answer by jorel555(1290)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x be your first alloy;
2/5x+7/10(30-x)=1/2(30)
4x+210-7x=150
3x=60
x=20
So, your need 20 lbs of the first alloy, and 10 parts of the second to make 30 lbs of half iron and half silver alloy!!!!!!!!!!
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One alloy is 2 parts iron to 3 parts silver and another alloy is 7 parts iron to 3 parts silver.
How much of each should be combined to produce a 30 pound alloy that is 1 part iron to 1 part silver?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "x" be an amount of the first alloy to be mixed (in pounds),
and "y" be an amount of the second alloy to be mixed (in pounds).
So, the "total mass equation" is
x + y = 30. (1)
The first alloy contains 2+3 = 5 parts of equal masses in total.
Of them, 2 parts is iron and 3 parts is silver.
So, the mass "x" of the first alloy contains  = 0.6x of silver.
The second alloy contains 7+3 = 10 parts of equal masses in total.
Of them, 7 parts is iron and 3 parts is silver.
So, the mass "y" of the second alloy contains = 0.6x of silver.
The second alloy contains 7+3 = 10 parts of equal masses in total.
Of them, 7 parts is iron and 3 parts is silver.
So, the mass "y" of the second alloy contains 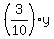 = 0.3y of silver.
Now, the "silver contents equation" is
0.6x + 0.3y = 0.5*30. (2)
0.5 on the right side means "half of mass" of the combined alloy.
Let's simplify equations (1) and (2) and write it together as a system.
x + y = 30. (1)
0.6x + 0.3y = 15. (2)
To solve it, express x = 30-y from (1) and substitute it into (2). You will get a single equation for y:
0.6*(30-y) + 0.3y = 15.
Simplify and solve it:
18 - 0.6y + 0.3y = 15,
3 = 0.3y,
y = 10.
So, 10 pounds of the 2-nd alloy should be taken, and, hence,
the amount of the 1-st alloy is 30 - 10 = 20 pounds.
Check: 20 pounds of the first alloy contain 3 parts of silver of the total 5 parts, i.e. 12 pounds of silver.
10 pounds of the second alloy contain 3 parts of silver of the total 10 parts, i.e. 3 pounds of silver.
12+3 = 15 pounds of silver in the combined/final alloy, which is precisely half of its mass.
The problem is solved. = 0.3y of silver.
Now, the "silver contents equation" is
0.6x + 0.3y = 0.5*30. (2)
0.5 on the right side means "half of mass" of the combined alloy.
Let's simplify equations (1) and (2) and write it together as a system.
x + y = 30. (1)
0.6x + 0.3y = 15. (2)
To solve it, express x = 30-y from (1) and substitute it into (2). You will get a single equation for y:
0.6*(30-y) + 0.3y = 15.
Simplify and solve it:
18 - 0.6y + 0.3y = 15,
3 = 0.3y,
y = 10.
So, 10 pounds of the 2-nd alloy should be taken, and, hence,
the amount of the 1-st alloy is 30 - 10 = 20 pounds.
Check: 20 pounds of the first alloy contain 3 parts of silver of the total 5 parts, i.e. 12 pounds of silver.
10 pounds of the second alloy contain 3 parts of silver of the total 10 parts, i.e. 3 pounds of silver.
12+3 = 15 pounds of silver in the combined/final alloy, which is precisely half of its mass.
The problem is solved.
|
|
|