Question 1032530: Pls help me solve this. this is the last equation for my homework.
Robert has 35 coins consisting dimes and quarters. If the total value is $5.90, how many of each kind of coin are there?
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! Robert has 35 coins consisting dimes and quarters.
d + q = 35 coins
---------------
If the total value is $5.90, how many of each kind of coin are there?
10d + 25q = 590 cents
-----
Modify for elimination::
d + q = 35
d + 2.5q = 59
---------
Subtract and solve for "q":
1.5q = 24
----
q = 16 (# of quarters)
d = 35-16 = 19 (# of dimes)
------------
Cheers,
Stan H.
------------
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
Pls help me solve this. this is the last equation for my homework.
Robert has 35 coins consisting dimes and quarters. If the total value is $5.90, how many of each kind of coin are there?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Or this another solution.
Let d be the number of dimes.
Then the number of quarters is 35-d.
The dimes contribute 10*d cents to the total.
The quarters contribute 25*(35-d) cents to the total.
As a result, the total is 10*d + 25*(35-d).
Since the total is 590 cents, it gives you an equation
10*d + 25*(35-d) = 590.
Simplify and solve it for d:
10d + 875 - 25d = 590,
10d - 25d = 590 -875,
-15d = -285,
d = 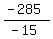 = 19.
So, there are 19 dimes.
Then the number of quarters is 35-19 = 16.
Answer. 19 dimes and 16 quarters.
|
|
|
