SOLUTION: How many liters each of a 35% acid solution and a 85% acid solution must be used to produce 50 liters of a 55% acid solution? (Round to two decimal places if necessary.)

Algebra ->  Customizable Word Problem Solvers  -> Mixtures -> SOLUTION: How many liters each of a 35% acid solution and a 85% acid solution must be used to produce 50 liters of a 55% acid solution? (Round to two decimal places if necessary.)      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1031498: How many liters each of a 35% acid solution and a 85% acid solution must be used to produce 50 liters of a 55% acid solution? (Round to two decimal places if necessary.)
Answer by ikleyn(52788) About Me  (Show Source):
You can put this solution on YOUR website!
.
How many liters each of a 35% acid solution and a 85% acid solution must be used to produce 50 liters of a 55% acid solution?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

Let x be the required volume of a 35% acid solution, in liters.

Then the volume of a 85% acid solution is (50-x)

The equation for the pure acid volume is 

0.35x + 0.85*(50-x) = 0.55*50.

Simplify and solve:

0.35x + 42.5 - 0.85x = 27.5,

-0.5x = 27.5 - 42.5,

-0.5x = -15,

x = 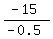%28-15%29%2F%28-0.5%29 = 30.

Answer. 30 liters of the 35% acid solution and (50-30) = 20 liters of the 85% acid solution is needed.