SOLUTION: mixing a given quantity of 30% silver alloy with a quantity of 90% silver yields 200 units of a 54% silver alloy. How many units of each alloy were used

Click here to see ALL problems on Mixture Word Problems

Question 1027852: mixing a given quantity of 30% silver alloy with a quantity of 90% silver yields 200 units of a 54% silver alloy. How many units of each alloy were used
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740) (Show Source):
You can put this solution on YOUR website!
Mixing a given quantity of 30% silver alloy with a quantity of 90% silver yields 200 units of a 54% silver alloy.
How many units of each alloy were used
:
:
let x = amt of 30% silver alloy
let y = amt of 90% silver alloy
:
Two equations
x + y = 200
x = (-y+200); we can use this form for substitution
and using the decimal equiv:
.30x + .90y = .54(200)
replace x with (-y+200)
.30(-y+200) + .90y = .54(200)
-.30y + 60 + .90y = 108
-.30y + .90y = 108 - 60
.60y = 48
y = 48/.60
y = 80 units of the 90% alloy
then
200 - 80 = 120 units of the 30% alloy
:
:
See if that checks out in the mixture equation
.30(120) + .90(80) = .54(200)
36 + 72 = 108; confirms our solutions

Answer by ikleyn(52786) (Show Source):
You can put this solution on YOUR website!
.
mixing a given quantity of 30% silver alloy with a quantity of 90% silver yields 200 units of a 54% silver alloy.
How many units of each alloy were used?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Let x = a mass of the 30% silver alloy used, and y = a mass of the 90% silver alloy used. Then the total mass equation is x + y = 200, and the "pure silver" mass equation is 0.3x + 0.9y = 0.54*200. Simplify these equations and collect them into a system of equations x + y = 200, (1) 0.3x + 0.9y = 108. (2) To solve it, express x = 200 - y from (1) and substitute it into (2). You will get a single equation for y: 0.3*(200 - y) + 0.9y = 108, 60 - 0.3y + 0.9y = 108, 0.6y = 108 - 60 ---> 0.6y = 48 ---> y = 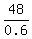= 80. Thus the mass of the 90% silver alloy used was 80 units. The mass of the 30% silver alloy used was 200-80 = 120 units.