SOLUTION: mr.henson needs 400 grams of a 45% solution of alcohol by mixing 35% and 75% solutions. How much of each does he need?

Let x be the mass of 35% solution (in grams) and y be the mass of 75% solution (in grams) to be mixed.


Looking for the total mass you have this equation: x + y = 400. 

Looking for the alcohol content you have the second equation: 0.35*x + 0.75*y = 0.45*400 = 180.


Combining both equations, you have this system of two equations in two unknowns

     x +      y = 400,   (1)
0.35*x + 0.75*y = 180.   (2).

To solve it, multiply equation (1) by 0.35 (all the terms in both sides) and then distract from the equation (2).
In this way you eliminate x and will obtain a single equation for y:

0.75*y - 0.35*y = 180 - 0.35*400,   or

0.4*y = 40.

Hence, y = 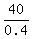 = 100.

Answer. 100 grams of 75% and 400-100 = 300 grams of 35% solutions are needed.