Lesson Wrapping a gift

This Lesson (Wrapping a gift) was created by by ikleyn(52778)

: View Source, Show
About ikleyn:

Wrapping a gift

Problem 1

A gift has the dimensions of 50 cm x 35 cm x 5 cm. You have wrapping paper with dimensions of 75 cm by 60 cm.
Do you have enough wrapping paper to wrap the gift?

Solution

Let's assume for a minute that such wrapping is possible.

I will show that it leads to a contradiction, which will prove that wrapping is not possible.

Let's assume that the box is wrapped.


Mark the point at the center of the 50 cm by 35 cm face of the box.


Using pencil, draw the straight segments along the longest path on the box surface until you return to the same point,
moving perpendicularly to 35 cm edges.


The length of this longest path is  25 + 5 + 50 + 5 + 25 = 110 centimetres.


If you then un-wrap the paper, you will get a straight line segment on it, whose total length is 110 centimetres.


But it is NOT POSSIBLE : the longest straight segment on this piece of paper is its diagonal, 

whose length is 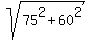  = 90.05 centimetres (rounded).


This contradiction PROVES my statement.

My other additional lessons on Miscellaneous word problems in this site are
    - I do not have enough savings now
    - In a jar, all but 6 are red marbles
    - How many boys and how many girls are there in a family ?
    - What is the last digit of the number a^n ?
    - Find the last three digits of these numbers
    - What are the last two digits of the number 3^123 + 7^123 + 9^123 ?
    - Advanced logical problems
    - Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b) and sqrt(c)
    - Calculus optimization problems for shapes in 2D plane
    - Calculus optimization problems for 3D shapes
    - Solving some linear minimax problems in 3D space
    - Solving one non-linear minimax problems in 3D space
    - Solving linear minimax problem in three unknowns by the simplex method
    - Advanced logical problems
    - In the worst case
    - Page numbers on the left and right facing pages of an opened book
    - Selected problems on counting elements in subsets of a given finite set
    - How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
    - Nice problems to setup them using Venn diagram
    - In preparation for Halloween
    - Nice entertainment problems related to divisibility property
    - Stars and bars method for Combinatorics problems
    - Math Olympiad level problem on caves and bats
    - Math Olympiad level problem on caught fishes
    - Math Olympiad level problem on pigeonhole principle
    - Math Olympiad level problem on placing books in bookcase
    - OVERVIEW of additional lessons on Miscellaneous word problems

Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.

Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

This lesson has been accessed 1172 times.