Lesson Tom the cat is brushing up his Math skills

Tom the cat is brushing up his Math skills

Problem 1

So, Tom wants to find the number , summation over all  even m from 0 to N  (from 0 to the largest even number lesser or equal to N).

For the solution, let us call this sum as 

 = , summation over all  even m from 0 to N  (from 0 to the largest even number lesser or equal to N).

    (index "e" is the first letter of the word "even").

Also, let us consider another sum, 

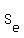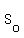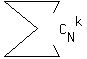 = , summation over all  odd k from 0 to N  (from zero to the largest odd number lesser or equal to N).

    (index "o" is the first letter of the word "odd").

Then these two equalities are true:

1) 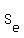  + 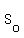 = ,     (1)    and

2) 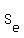  = 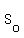.           (2)

Equality (1) is true, because its left side is the sum of all binomial coefficients of the binomial expansion .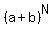
Then (1) is well known property of the sum of the binomial coefficients of the binomial expansion
(see the lesson The Pascal's triangle in this site).

The property (2) is also well known. It is read as "the alternate sum of the binomial coefficients is equal to zero"
and in this form it is also proved in the referred lesson.

Fantastic! Now from (1) and (2) we have   =  = .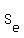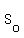

This is the solution, the result and the answer for the curious Tom the cat,
and this is the solution of the problem: The number under the question is equal to .

Isn't it a beautiful problem / solution / result ?