Stars and bars method for Combinatorics problems
The problems and the method of their solutions in this lesson are of highest peaks in Combinatorics.
They are at the level of a School Math circle at the local or (better to say) of a renowned University.
Problem 1
How many solutions (using only positive integers) are there to the following equation
x1 + x2 + x3 + x4 + x5 = 36 ?
Solution
x1 + x2 + x3 + x4 + x5 = 36 (1)
Imagine 36 marbles on the table, placed in one straight line with small gaps between them.
Imagine you have 6 numbered bars, of which you place the first bar (bar N1) before the first marble and the last bar (bar N6)
after the last marble in the row.
Let  ,
,  ,
,  ,
,  ,
, 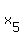 be some solution to the given equation.
You then place bar N2 after
be some solution to the given equation.
You then place bar N2 after  -th marble in the gap in the row of marbles;
then you count next
-th marble in the gap in the row of marbles;
then you count next  marbles in the row of marbles after bar N2 and place bar N3 in the gap there;
then you count next
marbles in the row of marbles after bar N2 and place bar N3 in the gap there;
then you count next  marbles in the row of marbles after bar N3 and place bar N4 in the gap there;
finally, you count next
marbles in the row of marbles after bar N3 and place bar N4 in the gap there;
finally, you count next  marbles in the row of marbles after bar N4 and place bar N5 in the gap there.
At this moment, all 36 marbles are divided in 5 groups between bars (1-2), (2-3), (3-4), (4,5) and (5,6).
So, having the solution to equation (1) in positive integer number, you place 4 bars N2, N3, N4 and N5 in their
corresponding positions in gaps in the row of marbles.
Vise versa, if you place 4 bars B2, B3, B4 and B5 in gaps in the row of 36 marbles, you divide marbles in 5 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in positive integer numbers,
from one side, and all different possible placings of 4 bars in gaps in the row of 36 marbles.
Also note that no one pair of bars goes to any single gap between marbles,
because the numbers
marbles in the row of marbles after bar N4 and place bar N5 in the gap there.
At this moment, all 36 marbles are divided in 5 groups between bars (1-2), (2-3), (3-4), (4,5) and (5,6).
So, having the solution to equation (1) in positive integer number, you place 4 bars N2, N3, N4 and N5 in their
corresponding positions in gaps in the row of marbles.
Vise versa, if you place 4 bars B2, B3, B4 and B5 in gaps in the row of 36 marbles, you divide marbles in 5 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in positive integer numbers,
from one side, and all different possible placings of 4 bars in gaps in the row of 36 marbles.
Also note that no one pair of bars goes to any single gap between marbles,
because the numbers  ,
,  ,
,  ,
,  ,
, 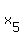 all are positive (!)
Thus, the number of solutions to equation (1) is equal to the number of COMBINATIONS of 35 (= 36-1) gaps taken 4 at a time.
Hence, the number of all possible solutions to equation (1) in positive integer numbers is equal to
all are positive (!)
Thus, the number of solutions to equation (1) is equal to the number of COMBINATIONS of 35 (= 36-1) gaps taken 4 at a time.
Hence, the number of all possible solutions to equation (1) in positive integer numbers is equal to  =
= 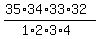 = 52360.
ANSWER. The number of different solutions to equation (1) is
= 52360.
ANSWER. The number of different solutions to equation (1) is  = 52360.
= 52360.
Solved.
------------------
More general problem to find the number of positive integer solution to equation
 +
+  +
+  + . . . +
+ . . . +  = n
where k <= n, can be solved in the same way and has the answer
= n
where k <= n, can be solved in the same way and has the answer 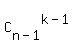 .
We have then (n-1) gaps between "n" "marbles" and (k-1) movable dividing bars.
The method I used in the solution is called the "method of bars and stars".
You can read about it in this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
.
We have then (n-1) gaps between "n" "marbles" and (k-1) movable dividing bars.
The method I used in the solution is called the "method of bars and stars".
You can read about it in this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
The second problem seems to be similar to the first one, but is different in some important aspects.
Problem 2
How many solutions (using non-negative integers) are there to the following equation
x1 + x2 + x3 + x4 + x5 = 36 ?
Solution
x1 + x2 + x3 + x4 + x5 = 36 (1)
Imagine 36 marbles on the table, placed in one straight line with small gaps between them.
Imagine you have 6 numbered bars, of which you place the first bar (bar N1) before the first marble and the last bar (bar N6)
after the last marble in the row.
Let  ,
,  ,
,  ,
,  ,
, 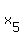 be some solution to the given equation.
You then place bar N2 after
be some solution to the given equation.
You then place bar N2 after  -th marble in the gap in the row of marbles;
then you count next
-th marble in the gap in the row of marbles;
then you count next  marbles in the row of marbles after bar N2 and place bar N3 in the gap there;
then you count next
marbles in the row of marbles after bar N2 and place bar N3 in the gap there;
then you count next  marbles in the row of marbles after bar N3 and place bar N4 in the gap there;
finally, you count next
marbles in the row of marbles after bar N3 and place bar N4 in the gap there;
finally, you count next  marbles in the row of marbles after bar N4 and place bar N5 in the gap there.
At this moment, all 36 marbles are divided in 5 groups between bars (1-2), (2-3), (3-4), (4,5) and (5,6).
Notice that if some
marbles in the row of marbles after bar N4 and place bar N5 in the gap there.
At this moment, all 36 marbles are divided in 5 groups between bars (1-2), (2-3), (3-4), (4,5) and (5,6).
Notice that if some  is zero, then the corresponding bars go to the common respective gap.
In particular, if
is zero, then the corresponding bars go to the common respective gap.
In particular, if  = 0, then the bars N1 and N2 are placed in one common gap close to each other BEFORE the first marble (!)
So, having the solution to equation (1) in non-negative positive integer number, you place 4 bars N2, N3, N4 and N5 in
their corresponding positions in gaps in the row of marbles.
Vise versa, if you place 4 bars B2, B3, B4 and B5 in gaps in the row of 36 marbles, you divide marbles in 5 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in non-negative integer numbers,
from one side, and all different possible placings of 4 bars in 36 gaps in the row between 36 marbles, plus one gap before the 1-st marble.
Thus we have 36+4 = 40 entities, 36 gaps and 4 bars; 36 gaps are indistinguishable and 4 movable bars
are indistinguishable, too.
The number of all possible indistinguishable arrangements of 40 items of two types with 36 indistinguishable of one type
and 4 indistinguishable of the other type is
= 0, then the bars N1 and N2 are placed in one common gap close to each other BEFORE the first marble (!)
So, having the solution to equation (1) in non-negative positive integer number, you place 4 bars N2, N3, N4 and N5 in
their corresponding positions in gaps in the row of marbles.
Vise versa, if you place 4 bars B2, B3, B4 and B5 in gaps in the row of 36 marbles, you divide marbles in 5 groups,
and the numbers of marbles in each group form the solution to equation (1).
Thus, there is one-to-one correspondence between the set of solutions to equation (1) in non-negative integer numbers,
from one side, and all different possible placings of 4 bars in 36 gaps in the row between 36 marbles, plus one gap before the 1-st marble.
Thus we have 36+4 = 40 entities, 36 gaps and 4 bars; 36 gaps are indistinguishable and 4 movable bars
are indistinguishable, too.
The number of all possible indistinguishable arrangements of 40 items of two types with 36 indistinguishable of one type
and 4 indistinguishable of the other type is 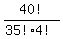 =
= 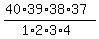 = 91390.
Hence, the number of all possible solutions to equation (1) in positive integer numbers is equal to
= 91390.
Hence, the number of all possible solutions to equation (1) in positive integer numbers is equal to 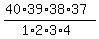 = 91390.
ANSWER. The number of different solutions to equation (1) is 91390.
= 91390.
ANSWER. The number of different solutions to equation (1) is 91390.
Solved.
------------------
More general problem to find the number of non-negative integer solution to equation
 +
+  +
+  + . . . +
+ . . . +  = n
where k <= n, can be solved in the same way and has the answer
= n
where k <= n, can be solved in the same way and has the answer 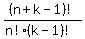 .
We have then n gaps between "n" "marbles" (including one gap BEFORE the first marble) and (k-1) movable dividing bars.
The method I used in the solution is called the "method of bars and stars".
You can read about it in this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
.
We have then n gaps between "n" "marbles" (including one gap BEFORE the first marble) and (k-1) movable dividing bars.
The method I used in the solution is called the "method of bars and stars".
You can read about it in this Wikipedia article
https://en.wikipedia.org/wiki/Stars_and_bars_%28combinatorics%29
My other additional lessons on Miscellaneous word problems in this site are
- I do not have enough savings now
- In a jar, all but 6 are red marbles
- How many boys and how many girls are there in a family ?
- What is the last digit of the number a^n ?
- Find the last three digits of these numbers
- What are the last two digits of the number 3^123 + 7^123 + 9^123 ?
- Advanced logical problems
- Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b) and sqrt(c)
- Calculus optimization problems for shapes in 2D plane
- Calculus optimization problems for 3D shapes
- Solving some linear minimax problems in 3D space
- Solving one non-linear minimax problems in 3D space
- Solving linear minimax problem in three unknowns by the simplex method
- The "pigeonhole principle" problems
- In the worst case
- Page numbers on the left and right facing pages of an opened book
- Selected problems on counting elements in subsets of a given finite set
- How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
- Nice problems to setup them using Venn diagram
- Wrapping a gift
- In preparation for Halloween
- Nice entertainment problems related to divisibility property
- Math Olympiad level problem on caves and bats
- Math Olympiad level problem on caught fishes
- Math Olympiad level problem on pigeonhole principle
- Math Olympiad level problem on placing books in bookcase
- OVERVIEW of additional lessons on Miscellaneous word problems
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.

