This Lesson (Prove that if a, b, and c are the sides of a triangle, then so are sqrt(a), sqrt(b) and sqrt(c)) was created by by ikleyn(52781)   : View Source, ShowAbout ikleyn:
Prove that if a, b, and c are the sides of a triangle, then so are 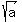 , , 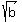 , and , and 
Problem 1Prove that if "a", "b", and "c" are the sides of a triangle, then so are 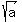 , , 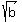 , and , and  . .
Proof
Let assume that
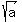 + + 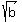 <= <=  . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, square both sides of (1). You will get
a + . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, square both sides of (1). You will get
a +  + b <= c, or
a + b <= c - + b <= c, or
a + b <= c -  .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES 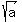 + + 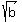 > >  .
It works for any combinations of sides of a triangle.
Thus we proved that the values .
It works for any combinations of sides of a triangle.
Thus we proved that the values 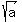 , , 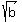 , ,  satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then 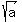 , , 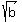 , and , and  form a triangle, too. form a triangle, too.
Problem 2Prove that if "a", "b", and "c" are the sides of a triangle, then so are 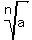 , ,  , and , and  for any integer positive index n >= 2. for any integer positive index n >= 2.
Proof
For n= 2 it is just proved in Problem 1 above.
So I will assume here that n >= 3.
Let assume that
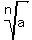 + +  <= <=  . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, raise both sides of (1) to degree n. You will get
a + . (1)
where "a", "b" and "c" are the sides of a triangle.
I want to lead it to CONTRADICTION.
Indeed, raise both sides of (1) to degree n. You will get
a + 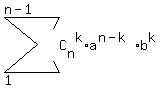 + b <= c, or
a + b <= c - + b <= c, or
a + b <= c - 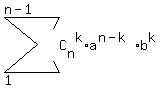 .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES .
Then even more so
a + b < c.
But it contradicts to the triangle inequality a + b > c.
Thus we proved that a + b > c IMPLIES 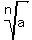 + +  > >  .
It works for any combinations of sides of a triangle.
Thus we proved that the values .
It works for any combinations of sides of a triangle.
Thus we proved that the values 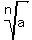 , ,  and and  satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then satisfy all triangle inequalities,
if "a", "b" and "c" are the sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then 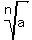 , ,  and and  form a triangle, too. form a triangle, too.
Problem 3Let f: R+ ---> R+ be a monotonically risen one-to-one function such that f(a) + f(b) > f(a+b) for all real positive numbers "a" and "b".
Prove that if "a", "b", and "c" are the sides of a triangle, then so are f(a), f(b), and f(c).
Proof
Let "a", "b", and "c" are the sides of the triangle.
Then for any combination of sides, we have the "triangle inequality
Let assume that
a + b > c. (1)
It implies
f(a) + f(b) > f(a+b) due to the property of the function f(x), and then
f(a+b) > f(c) due to monotonity of the function f(x).
Thus we proved that a + b > c implies that f(a) + f(b) > f(c).
So, we proved that if "a", "b" and "c" are the sides of a triangle, then the values f(a), f(b) and f(c) satisfy triangle inequalities.
It works for any combinations of sides of a triangle.
It implies that if "a", "b" and "c" are the sides of a triangle, then f(a), f(b) and f(c) form a triangle, too.
My other additional lessons on Miscellaneous word problems in this site are
- I do not have enough savings now
- In a jar, all but 6 are red marbles
- How many boys and how many girls are there in a family ?
- What is the last digit of the number a^n ?
- Find the last three digits of these numbers
- What are the last two digits of the number 3^123 + 7^123 + 9^123 ?
- Advanced logical problems
- Calculus optimization problems for shapes in 2D plane
- Calculus optimization problems for 3D shapes
- Solving some linear minimax problems in 3D space
- Solving one non-linear minimax problems in 3D space
- Solving linear minimax problem in three unknowns by the simplex method
- The "pigeonhole principle" problems
- In the worst case
- Page numbers on the left and right facing pages of an opened book
- Selected problems on counting elements in subsets of a given finite set
- How many integer numbers in the range 1-300 are divisible by at least one of the integers 4, 6 and 15 ?
- Nice problems to setup them using Venn diagram
- Wrapping a gift
- In preparation for Halloween
- Nice entertainment problems related to divisibility property
- Stars and bars method for Combinatorics problems
- Math Olympiad level problem on caves and bats
- Math Olympiad level problem on caught fishes
- Math Olympiad level problem on pigeonhole principle
- Math Olympiad level problem on placing books in bookcase
- OVERVIEW of additional lessons on Miscellaneous word problems
Use this file/link ALGEBRA-I - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-I.
Use this file/link ALGEBRA-II - YOUR ONLINE TEXTBOOK to navigate over all topics and lessons of the online textbook ALGEBRA-II.
This lesson has been accessed 1234 times.
|

