Lesson One unusual mimimax problem on joint work

One unusual mimimax problem on joint work

Problem 1

1.  Let us assign Nicolai to paint the walls, and let us assign Elena to paint the ceiling.

    After 1 hour working, Elena will complete painting ceiling.

    During this 1 hour Nicolai will complete painting of 2/3 of walls.

    Then Elena will switch for painting the walls with Nikolai.

    Their combined rate of work painting the walls is 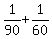 =  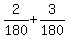=  =  of the walls surface per  minute.

    Hence, it will take 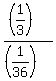 =  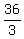= 12 minutes for them to complete the job painting the remaining  of the wall surface.
    
    Last calculation 60 minutes + 12 minutes = 72 minutes gives you the ANSWER.



2.  In n.1 I simply "guessed" the right solution.

    Now I want to show you how to derive it MATHEMATICALLY.


    In the general case, let "w" and "c" be two real numbers between 0 and 1:  0 <= w, c <= 1.


    Let us assign Nicolai to paint w-th part of the wall area and c-th part of the ceiling.

    Accordingly, Elene will paint (1-w)-th part of the wall area and (1-c)-th part  the ceiling.

    Our task is to chose the values w and c in a way to minimize the total time.

    The necessary condition for it is THIS:


        Nicolai and Elena should complete their personal assignments SIMULTANEOUSLY.           (*)


    I will leave this statement without the proof (because it is self-evident).

    It is self-evident, but EXTREMELY helpful.


3.   Now let see what does it mean in a quantitative sense.

     The time for Nicolai to complete his assignment is 90*w + 120*c minutes  (90 is 90 minutes = 1.5 hours and 120 = 120 minutes = 2 hours).

     The time for Elena   to complete her assignment is 60*(1-w) + 60*(1-c) minutes  (60 is 60 minutes = 1 hour and 60 = 60 minutes = 1 hour).

     The condition (*) gives you an equation

         90*w + 120*c = 60*(1-w) + 60*(1-c),

     which you can simplify to the form

         5w + 6c = 4.     (1)


     So, you see that the optimal solution must obey to the condition (1) to provide the minimal time.



4.  Now, the time that Nicolai will spend for his personal assignment is 

    N = 90w + 120c = 90w + 108c + 12c = 18*(5w + 6c) + 12c = 18*4 + 12c = 72 + 12c.

    And you see that N is always greater than 72, if c > 0.

    So, to provide minimal time 72 minutes for Nicolai, the value of "c" must be ZERO.


    Thus we get this solution  w = , c = , which I "guessed" in n.1.

    Now it is DERIVED with mathematical precision.