Question 999941: Why are these two similar problems set up differently? and why are they set up in that way at all?
Find two numbers whose difference is 60 and whose product is a minimum? Why does this use f(x) = x(x-60)
and
Find two numbers whose sum is 60 and whose product is a maximum? Why does this one use f(x) = x(60-x)
I fundamentally don't understand what is happening and how that function was created at all.
And will there ever be a case where it's a difference and the product is a maximum. Or where it's a sum and the product is a minimum. I don't understand what this question is asking.
So confused...
Please help!
Found 2 solutions by Fombitz, MathTherapy:
Answer by Fombitz(32388)   (Show Source): (Show Source):
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Why are these two similar problems set up differently? and why are they set up in that way at all?
Find two numbers whose difference is 60 and whose product is a minimum? Why does this use f(x) = x(x-60)
and
Find two numbers whose sum is 60 and whose product is a maximum? Why does this one use f(x) = x(60-x)
I fundamentally don't understand what is happening and how that function was created at all.
And will there ever be a case where it's a difference and the product is a maximum. Or where it's a sum and the product is a minimum. I don't understand what this question is asking.
So confused...
Please help!
1st problem:
Let larger number be x, and smaller, y
Then we have: x - y = 60______y = x - 60 ------- eq (i)
Also, y = xy ------- eq (ii)
y = x(x – 60) ------- Substituting x – 60 for y in eq (ii)
 --------- eq (ii) --------- eq (ii)
MINIMUM occurs at:  , or at: , or at:  , or at , or at  , or at: x = 30 , or at: x = 30
With MINIMUM occurring at x = 30, we get:
y = 30 – 60 ----------- Substituting 30 for x in eq (i)
y = - 30
As seen, the numbers that differ by 60, and have a MINIMUM product are: 
MINIMUM: 30(- 30), or - 900
2nd problem:
Let larger number be x, and smaller, y
Then we have: x + y = 60_____y = 60 - x ------- eq (i)
Also, y = xy ------- eq (ii)
y = x(60 - x) ------ Substituting 60 – x for y in eq (ii)

MAXIMUM occurs at:  , or at: , or at:  , or at , or at  , or at x = 30 , or at x = 30
With MAXIMUM occurring at x = 30, we get:
y = 60 - 30
y = 30
As seen, the numbers that sum to 60, and that have a MAXIMUM product are the same, at: 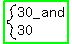
MAXIMUM: 30(30), or 900
|
|
|