Question 988618: A man spends money according to the date.
Eg: On 15th he will spend 15rs, 19th he will spend 19rs.
One night he will count 5 consecutive days and the amount equals to 61.
What are those 5 consecutive dates?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The five consecutive dates are:
February 27, February 28, March 1, March 2, and March 3 of a year that is not a leap year.
Five consecutive days often will be in the same month and hence consecutively numbered, as in
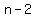 , , 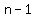 , ,  , ,  , and , and  , which add up to , which add up to
 , so the sum would be a multiple of 5. , so the sum would be a multiple of 5.
Since 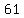 is not a multiple of 5, is not a multiple of 5,
the 5 consecutive days must include the end of a month and the beginning of the next month.
If the first month  or or 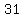 days, days,
the possible sums do not add up to 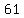 : :
 , ,  , ,
 , ,  . .
So, the first month must be February, with 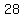 or or  days. days.
Since  and and  , ,
the sum  works. works.
The other possibility with two days in February and three in March,
 , yields a sum that is too high, , yields a sum that is too high,
and using only one day from February will yield too low a sum.
|
|
|