Question 936620: For the following polynomials , find all real and complex roots .(hint: Use the rational root theorem to identify potential roots.
1- y(x) = x^3-1
2- h(x) = x^4 -1
3- g(x) = x^4 +2x^3-16x^2-2x+15
4- f(x) = x^4+ 2x^3 -16x^2 -2x +15
(note:what they mean by potential roots?) .Thanks
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! to identify POTENTIAL roots use THE RATIONAL ZERO THEOREM
If  = =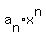 + .... .+ + .... .+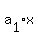 + +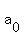 has integer coefficients, then every rational zero of has integer coefficients, then every rational zero of  has the following form: has the following form:

using that, we have:
1- 
--> factor  and and  : :
 = ± = ± which is which is  = ± = ±
2- 
--> factor  and and  : :
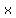 = ± = ± which is which is  = ± = ±
3- 
--> factor  , and , and  : :
 X X  , , , , , ,
 = ± = ± , ± , ±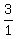 ,± ,± ,± ,± , which is => , which is =>  = ± = ± ,± ,± ,± ,± ,± ,±
Test these zeros using synthetic division.
test 

 |--1-----2----..-16------...-2----15 |--1-----2----..-16------...-2----15
---| ------1----..-1----..-1------17---..-15
---| 1---- 1----.. -17--------15------- 0
so,  is the root is the root
same way you check all other potential roots
now find roots:
1-  ........factor: set ........factor: set  and use and use  ..(difference of ..(difference of  cubes rule) cubes rule)

we already know one root: if  => => 
use quadratic formula to find other two roots from  : :




solution will be complex roots:

and

2- 




roots:
 => =>
 => => ......real roots ......real roots
 => =>  => =>  => =>  or or 
 .........complex roots .........complex roots

3-  ...write ...write 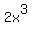 as as 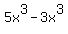 and and 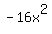 as as 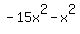
 ....group ....group


 ...group ...group



roots:
 => => 
 => => 
 => =>
 => =>  ........all roots are real roots ........all roots are real roots

4-  this is same as 3- this is same as 3-
|
|
|