Question 934770: Can someone please help me!!
It took a small plane 2 h longer to fly 375 mi against the wind than it took the plane to fly the same distance with the wind. the rate of the wind was 25 mph. find the rate of the plane in calm air.
Found 3 solutions by stanbon, josgarithmetic, MathTherapy:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! It took a small plane 2 h longer to fly 375 mi against the wind than it took the plane to fly the same distance with the wind. the rate of the wind was 25 mph. find the rate of the plane in calm air.
----------------------
Against wind DATA:
time = x+2 hrs ; distance = 375 miles ; rate = d/t = 375/(x+2) mph
-----
With wind DATA:
time = x hrs ; distance = 375 miles ; rate = d/t = 375/x mph
----
Equation:
Against wind:: p-25 = (375/(x+2))
With wind:: p + 25 = 375/x
-----
Subtract and solve for "x"::
375/x - 375/(x+2) = 50
----
375(x+2) - 375x = 50x(x+2)
---------
750 = 50x^2 + 100x
-----
x^2 + 2x - 15 = 0
(x+5)(x-3) = 0
Positive solution::
x = 3 hrs
----
Rate of plane in calm air = 375/x = 375/3 = 125 mph
-----------------------
Cheers,
Stan H.
----------------
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! r, rate of plane in calm air
w, speed of the wind. Let w=25 mph.
t, time of travel with the wind
v, quantity of time in excess of t. Let v=2 hours.
q, quantity of distance against the wind. Let q=375 miles.
Also, q is the quantity of distance flown with the wind.
______________________speed___________time______________distance
AGNST_________________(r-w)___________t+v________________q
WITH__________________(r+w)____________t_________________q
The idea in this way is to keep everything in symbols, and save all computations for later. This is not always necessary. The only two unknown variables are r and t. Use the travel rate equation to form two equations for against and for with, the wind.

Solve the system for r, and its value. This just requires several arithmetic, or algebra steps.
 , but the second equation here was better in its original form. You want to substitute for t. , but the second equation here was better in its original form. You want to substitute for t.
The WITH equation is also  . Substitute into "first" equation, the AGAINST one. . Substitute into "first" equation, the AGAINST one.







You could keep going completely in symbols, but now would be a good place for the next step to plug in the known values, AND THEN finish the solving of this quadratic equation for r. Note, the question asks for r, the rate of the plane in calm air, and r is the only variable UNKNOWN in this quadratic equation. You would then use general solution ....
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Can someone please help me!!
It took a small plane 2 h longer to fly 375 mi against the wind than it took the plane to fly the same distance with the wind. the rate of the wind was 25 mph. find the rate of the plane in calm air.
Let speed of plane, in calm air be S
Since wind speed = 25 mph, then speed against wind = S 25, and speed with wind = S + 25
Time taken to travel 375 mls, against the wind: 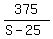
Time taken to travel 375 mls, with the wind: 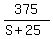
Since time taken to cover distance, travelling against the wind, is 2 hours greater than time taken to
cover distance travelling with the wind, then we can say that:

375(S + 25) 2(S 25)(S + 25) = 375(S 25) ------- Multiplying by LCD, (S 25)(S + 25)






S, or speed of plane in calm air = 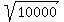 , or , or  mph mph
You can do the check!!
===================
Send comments, thank-yous, and inquiries to D at MathMadEzy@aol.com.
Further help is available, online or in-person, for a fee, obviously.
For FREE info and answers to questions about the ASVAB exam, the NYS 3 8 city/state wide exams,GENERAL
MATH and HOMEWORK QUESTIONS, or MATH QUESTIONS related to the Regents Integrated Algebra,
Regents Geometry, Regents Algebra 2/Trigonometry, SHSAT, COOP/HSPT/TACHS, PSAT, SAT, ACT, SSAT/ISEE,
GRE, CLEP, and the TASC/GED, you can visit: http://asvabstudyzone.freeforums.net/.
|
|
|