Question 887041: A good train running at 36 km/hr. takes 20 sec. to pass a platform. then it takes 12 sec. to pass a cyclist travelling at 18 km/hr. in the opposite direction. find the length of the train and that of the platform.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! 36 kmph / 3600 = .01 kmps
18 kmph / 3600 = .005 kmps
kmph = kilometers per hour
kmps = kilometers per second
train travels at .01 kmps
cyclist travels at .005 kmps
formula if r*t=d where:
r = rate
t = time
d = distance
we look at the cyclist first.
the train is traveling at .01 kmps in one direction and the cyclist is traveling at .005 kmps in the other direction.
the net speed of the train relative to the cyclist is equal to .01 + .005 = .015 kmps.
what this means is that, if the cyclist was standing still, the train would be traveling past it at .015 kmps.
in order to pass the cylist, the back of the train has to pass the cyclist 12 seconds after the front of the train passed it.
in 12 seconds, the front of the train has traveled .015 kmps * 12 = .18 km.
in 12 seconds, the back of the train has passed the cyclist.
this means that the length of the train had to be .18 km.
you can also look at the cyclist and train distances separately and should come up with the same conclusion.
the front of the train passes the cyclist at time point 0.
in 12 seconds, the train has traveled .01 * 12 = .12 km in one direction.
in 12 seconds, the cyclist has traveled .005 * 12 = .06 km in the other direction.
in 12 seconds, the back of the train has passed the cyclist.
since the front of the train has traveled .12km and at the same time the cyclist has traveled .06 km in the opposite direction, the length of the train has to be .06 + .12 = .18.
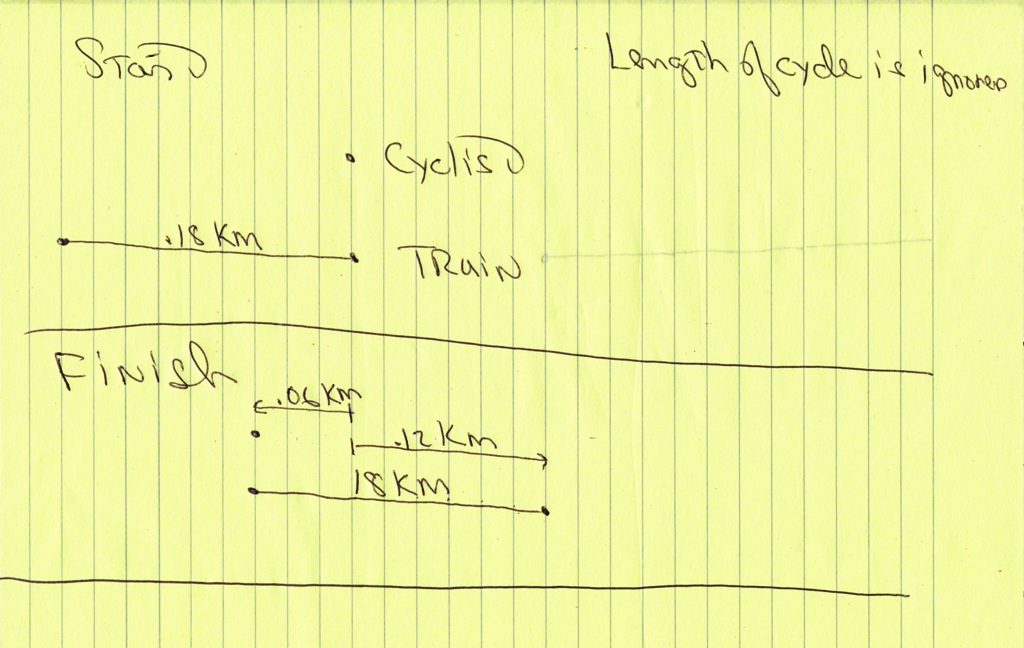
the following picture should help visualize what is happening.
at the start, the front of the train is even with the cyclist.
at the finish, the back of the train is even with the cyclist.
the train has to be .18 km in length
no that we know the length of the train, we can solve for the length of the platform.
the train passes the platform in 20 seconds.
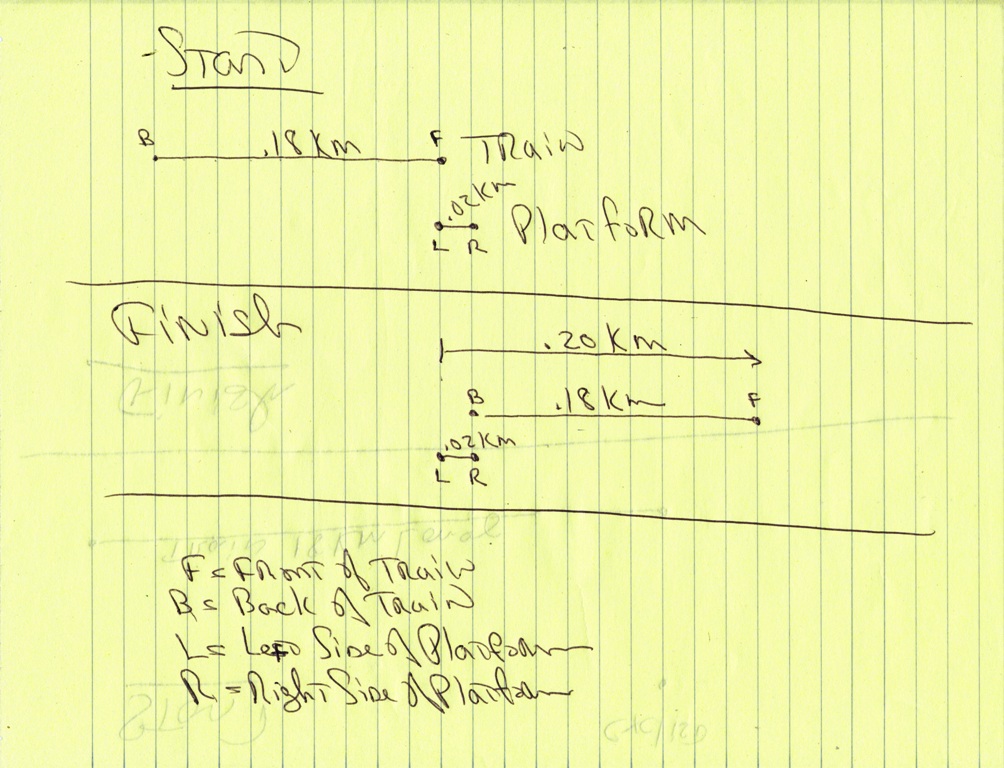
at the start, the front of the train is even with one end of the platform.
at the finish, the back of the trian is even with the other end of the platform.
in 20 seconds, the train has traveled 20 * .01 = .2 km.
the distance the train has traveled is x + .18
x is the length of the platform and .18 is the length of the train.
formula of rt*d becomes .01 * 20 = x + .18
solve for x to get x = .02
the length of the platform has to be .02 km.
the following picture should help visualize what is happening.
solution is:
length of train is .18 km
length of platform is .02 km.
there are approximately 3280.84 feet per km.
length of the train is about 591 feet long.
length of the platform is about 66 feet long.
|
|
|