Question 886544: I have combination word problem - 12 people are at a party and they all exchange handshakes. How many handshakes are exchanged?
Would this be 12! ? Or would that be overcounting and it need to be reduced?
Thank you for your help.
Found 2 solutions by josgarithmetic, MathTherapy:
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! Do this yourself through inductive thinking. Start with just three people. How many handshakes? To do this, draw the vertices of a triangle (three points, regular polygon). Next, draw the four vertices of a square, and assuming each point represents a person, draw and count all the handshakes. How many handshakes? Keep going; now, the vertices of a pentagon. How many handshakes? Pentagon shape vertices? How many handshakes? Keep doing this. Look for a rule inductively for vertices and "handshakes".
Also, look at the Mesh part of the article, http://en.wikipedia.org/wiki/Fully_connected_network#Mesh
Answer by MathTherapy(10551)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have combination word problem - 12 people are at a party and they all exchange handshakes. How many handshakes are exchanged?
Would this be 12! ? Or would that be overcounting and it need to be reduced?
Thank you for your help.
All this involves is the number of groups of 2 that can be formed by 12 people, and as person 1 doesn't shake
hands with him/her self, and since person 1 shaking hands with person 2 is the same as person 2 shaking hands
with person 1, order is UNIMPORTANT, thereby leading to the calculation of the combination of 12 persons,
choosing 2, or 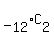 , or , or  handshakes. handshakes.
|
|
|