Question 826261: the area of a rectangle is 270cm^2. If the shorter side was reduced by 2cm and the longer side was increased by 16 cm^2. Find the lengths of the sides of the original rectangle.
Note the book says 16cm^2
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! The book is wrong. The item should go this way:
"The area of a rectangle is 270cm^2. If the shorter side was reduced by 2cm and the longer side was increased by 16 CM, find the lengths of the sides of the original rectangle."
So you have two lengths, x and y.
 ; ;
Then the IF part, x-2 for one length, and y+16 for the other length. "Find the lengths" or values of x and y.
That is, what is (x-2)(y+16) and how does it compare to xy=270? The item still seems missing something.
 , STILL A VARIABLE EXPRESSION. What is it supposed to be equal to? Not given. Not described enough. , STILL A VARIABLE EXPRESSION. What is it supposed to be equal to? Not given. Not described enough.
That is as far as can be done! (See "Further Thought").
-------------Further Thought-------------
Along with  , also is , also is  . .
Working with these,
y=270/x and 8x-y+119>0,  , ,
and substituting for y, obtain  . We expect that x>0, so if multiply both sides by x, we have no change in order relation: . We expect that x>0, so if multiply both sides by x, we have no change in order relation:
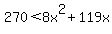

 , which we CAN work with. , which we CAN work with.
'
x critical points are  and and  ; ;
Discriminant is 22801.

'
Then the critical points, x are 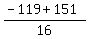 and and 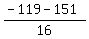 , only the positive one making sense for the problem. , only the positive one making sense for the problem.
'
 ; ;
 . .
Still unfinished for y, but maybe you could finish this.
|
|
|