Question 775825: What is the rate percent per annum if a sum of money doubles itself in 17 years at compound interest?
Can you plz show how to do it without using calculator?
Answer by josgarithmetic(39616)   (Show Source): (Show Source):
You can put this solution on YOUR website! The idea should be well enough explained in the books. It works this way:
You put some money in the account, quantity P. That quantity gains some interest at a rate, which we can call r. This r is a percent quantity. This r is used as a decimal number and not in percent units. Your first year for this account lets the account earn interest. This interest quantity is P*r. Every year, the interest the account earns will be P*r. If the account stays for n years, then the amount of interest, if r does not change, will be n*P*r.
COMPOUNDING?
Does this account compound it interest? This is more typical of accounts like what you have or put in the bank, and some other kinds. This means that the interest will be based on the compounding period and the amount of principle PLUS interest in the account. The principle is increased each compounding term (a time quantity).
'
If your compounding period is 1 year, then your growth of principle based on interest rate and compounding period is like this:
'
P = initial principle invested
r = interest rate as a decimal number (like 2.5% would be 0.025,...)
The first year, account quantity becomes P+P*r.
The second year, n=2, the account quantity becomes 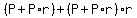 . .
At end of n=3, the account becomes  . .
And the increase continues this way.
Another way to understand this growth, easier to express, is that the rate each compounding term can be shown as a factor, (1+r), where "1" is for 100 percent, and the "r" is still the same rate percent; but the 1 and the r are still in their decimal form.
The BALANCE at the end of every term will be P(1+r), and of course, P always changes. If you wish showing P as the original principle amount, then the year by year balance will work like this:
Year Number_________Balance
0___________________P
1___________________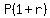
2___________________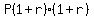
3___________________
.
.
n___________________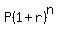
In there, n = the number of compounding periods. r is the rate for the compounding period length.
|
|
|