Question 74388: Any help here I am the worst with math problems.
Find the product of (x2 - 3x + 5) with the quotient of (18x6 - 27x5 - 9x3) ÷ 9x3.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Find the product of (x^2 - 3x + 5) with the quotient of (18x^6 - 27x^5 - 9x^3) ÷ 9x^3.
.
First we'll work on finding the quotient of:
.

.
You do that by dividing the denominator into each of the terms in the numerator, so your
answer has three terms. And the way you do the division is you divide the 9 into the number
in the term and you also subtract the exponents on their exponents of x. So to divide
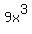 into into 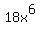 you divide the 9 into the 18 to get 2, and then you subtract you divide the 9 into the 18 to get 2, and then you subtract
the exponents of the x terms to get as the x part of the answer  . .
Putting this together results in the division of the first term by the denominator
being 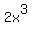
.
We use the same process to divide 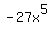 by by 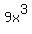 . Divide the 9 into the -27 and . Divide the 9 into the -27 and
get -3. Then divide the  into the into the 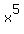 and get and get  . .
Put these two divisions together and the answer for the second term is 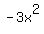 . .
.
And finally, divide the 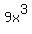 into the third term into the third term 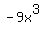 . The 9 into the -9 results . The 9 into the -9 results
in -1 and the  into the into the  results in results in  and by definition and by definition
anything raised to the 0 power is 1. So the answer for this division is -1 times 1 or
just -1.
.
Putting all three terms together, the quotient is 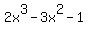 . Halfway home to being . Halfway home to being
done.
.
Next the problem requires that this quotient be multiplied by 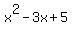
You can do
this by picking one term in the quotient and multiplying it by all the terms in 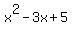 . .
You will get 3 answers. Then you pick a second term from the quotient and multiply it
by all three terms in 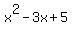 to get 3 more answers. Finally, you take the final to get 3 more answers. Finally, you take the final
term in the quotient and multiply it by all three terms in 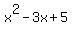 to get the final to get the final
group of 3 answers. Then you add all 9 answers together, look for common terms that can be
combined, combine them and what you end up with is the answer to the problem.
.
Before we begin this process, let's establish the multiplication ground rules. Just the opposite
of the division process. This time we multiply the numbers, not divide them. And we add
the exponents, not subtract them.
.
OK, let's go. From the quotient let's first take the term 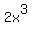 and we'll multiply it and we'll multiply it
by all the terms in 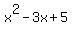 . The first multiplication is of . The first multiplication is of 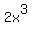 times times
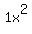 and the answer is and the answer is 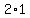 times times  to give us to give us 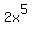 . .
The next multiplication is 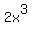 times times 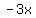 and its answer is and its answer is 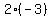
and  which gives us a total result of which gives us a total result of  . And finally we . And finally we
multiply 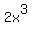 times times 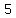 which results in which results in  and and  for for
an answer of 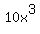 . We now have the first 3 of the 9 multiplication answers and . We now have the first 3 of the 9 multiplication answers and
they are 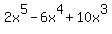 . .
.
Next we take the second term from the quotient. It is 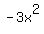 and we multiply it and we multiply it
by all three terms in 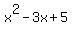 . Maybe by now you have enough of the idea to see . Maybe by now you have enough of the idea to see
that the three answers are 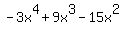 . (Multiply the coefficients and add the . (Multiply the coefficients and add the
exponents for each term.)
.
Finally multiply the last term of the quotient  and multiply it by each term in and multiply it by each term in
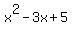 and you get and you get 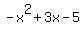 for these 3 answers. for these 3 answers.
.
So in one long string the answers are:
.
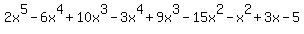
.
You have 2 terms containing  . They are . They are  and and 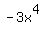 . Combine them . Combine them
into 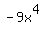 . You also can combine the . You also can combine the  terms. terms.  . And you . And you
can combine the  terms. terms.  . None of the other terms can . None of the other terms can
be combined so the resulting string of terms is:
.
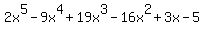 and that should be the answer to this problem. and that should be the answer to this problem.
.
It's been a long journey. I hope that this exercise has given you some insight into multiplying
and dividing algebraic terms and how you combine terms that have like powers of x.
|
|
|