SOLUTION: This one is kinda urgent..please i will appreciate ANY kind of help- "Imagine that you are on a street with houses marked 1 through n. There is a house in between (x) such that

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: This one is kinda urgent..please i will appreciate ANY kind of help- "Imagine that you are on a street with houses marked 1 through n. There is a house in between (x) such that       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 694702: This one is kinda urgent..please i will appreciate ANY kind of help-
"Imagine that you are on a street
with houses marked 1 through n. There is a
house in between (x) such that the sum of
the house numbers to left of it equals the
sum of the house numbers to its right. If n is
between 50 and 500, what are n and x?"
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I do not see the whole elegant solution, but maybe this helps.
A sum of consecutive house numbers is the sum of an arithmetic sequence/progression, which can be calculated as the average of the first and last terms, times the number of terms.
The sum of the numbers of the houses to one side is
1+2+3+ ... +(x-2)+(x-1)=%281%2B%28x-1%29%29%28x-1%29%2F2=x%28x-1%29%2F2
The sum of the numbers of the houses to the other side is
(x+1)+(x+2)+ ... +(n-1)+n=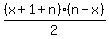%28x%2B1%2Bn%29%28n-x%29%2F2

So x%28x-1%29%2F2=%28x%2B1%2Bn%29%28n-x%29%2F2 --> x%28x-1%29=%28x%2B1%2Bn%29%28n-x%29 --> x%5E2-x=n%5E2%2Bn-n%5E2-x --> 2x%5E2=n%5E2%2Bn --> 2x%5E2=n%28n%2B1%29
Since they are consecutive integers,
n and n%2B1 cannot have any common factors.
For their product to be twice a perfect square, we need two perfect squares with no common factors:
one perfect square will be a factor of n,
and another perfect square will be a factor of n%2B1
Calling the larger one a%5E2,
either system%28n=a%5E2%2C%28n%2B1%29%2F2=b%5E2%29 --> 2b%5E2=a%5E2%2B1 <--> a%5E2=2b%5E2-1,
or system%28n%2F2=b%5E2%2Cn%2B1=a%5E2%29 --> 2b%5E2%2B1=a%5E2,
for some mutually prime positive integers a and b, with a%3Eb
whose squares must be between 25=50%2F2 and 501
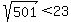Since sqrt%2825%29=5 and sqrt%28501%29%3C23, we should look at numbers from 5 to 22.
As the larger square a%5E2 is an odd number a%5E2=2b%5E2+%2B-+1, a is an odd number, and cannot be 22, so we should look at numbers from 5 to 22.
We are looking for a pair such that the square of the larger number is one more or one less than double the square of the smaller number.
We try numbers from 5 on as the smaller number b, and see what works.
I tried them making a table, which is hard for me to render here, so I will just show the calculations.
b=5 --> 2b%5E2=2%2A5%5E2=50 --> 2b%5E2-1=49%3C50 and 2b%5E2%2B1=51=not a square
b=6 --> 2b%5E2=2%2A6%5E2=72 --> 2b%5E2-1=71=not a square and 2b%5E2%2B1=73=not a square
b=7 --> 2b%5E2=2%2A7%5E2=98 --> 2b%5E2-1=97=not a square and 2b%5E2%2B1=99=not a square
b=8 --> 2b%5E2=2%2A8%5E2=128 --> 2b%5E2-1=127=not a square and 2b%5E2%2B1=129=not a square
b=9 --> 2b%5E2=2%2A9%5E2=162 --> 2b%5E2-1=161=not a square and 2b%5E2%2B1=163=not a square
b=10 --> 2b%5E2=2%2A10%5E2=200 --> 2b%5E2-1=199=not a square and 2b%5E2%2B1=201=not a square
b=11 --> 2b%5E2=2%2A11%5E2=242 --> 2b%5E2-1=241=not a square and 2b%5E2%2B1=243=not a square
b=12 --> 2b%5E2=2%2A6%5E2=288 --> 2b%5E2-1=287=not a square and 2b%5E2%2B1=highlight%28289=17%5E2%29
The pair b=12 and a=17 with a%5E2=2b%5E2%2B1 , works with system%28n%2F2=b%5E2%2Cn%2B1=a%5E2%29,
so n%2B1=a%5E2 --> n%2B1=17%5E2 --> n%2B1=289 --> highlight%28n=288%29
and 2x%5E2=n%28n%2B1%29 --> 2x%5E2=288%2A289 --> x%5E2=288%2A289%2F2 --> x%5E2=%0D%0A41616 --> highlight%28x=204%29

Since we expect only one solution, we could stop here.
Otherwise we would try further to see that nothing else works.
b=13 --> 2b%5E2=2%2A13%5E2=339 --> 2b%5E2-1=337=not a square and 2b%5E2%2B1=339=not a square
b=14 --> 2b%5E2=2%2A14%5E2=392 --> 2b%5E2-1=391=not a square and 2b%5E2%2B1=393=not a square
b=15 --> 2b%5E2=2%2A15%5E2=450 --> 2b%5E2-1=449=not a square and 2b%5E2%2B1=451=not a square
b%3E=16 --> 2b%5E2%3E=2%2A16%5E2=512 --> 2b%5E2%2B1%3E2b%5E2-1%3E=511%3E501=not a number that could be n or n%2B1