Question 678589: John and jane have their birthday today. in 3 yrs, john will be four times as old as jane was when john was 2 years older than jane is today. Find john's age if jane is a teenager?
i am going around in circles with this! please help??
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The systematic approach to the problem would be as follows.
STEP 1 - Define variables and understand what values they can and cannot take
 = John's age (That's how old John is today) = John's age (That's how old John is today)
 = Jane's age (That's how old Jane is today) = Jane's age (That's how old Jane is today)
 = the difference in their ages = the difference in their ages
John was, is, and will be  years older than Jane. years older than Jane.
I am interpreting "was" as indicating the past,
meaning that John, who "was 2 years older than Jane is today,"
is now older than that, so he is more than 2 years older than Jane,
so 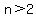 . .
Jane is a teenager, so 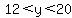 , ,
because the only numbers that end in "teen" are thirteen (13) to nineteen (19).
STEP 2 - Translate phrases into algebraic expressions or equations.
John's age now is  , because , because
 <--> <--> 
In 3 years, John will be 
When John was 2 years older than Jane is today, he was 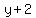 . .
At that point Jane (always  years younger) was years younger) was 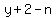
Four times that is 
In 3 years, John will be  , ,
and that number is  , ,
so 
STEP 3 - See what you can do with the information
We have
 , ,
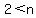 , ,
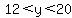 , and , and
 <--> <-->  <--> <-->  <--> <-->  <--> <-->  <--> <--> 
and the fact that all variables are integers.
If we want a formula to calculate  we can get we can get  --> {{x=8y/5+1}}} --> {{x=8y/5+1}}}
We could try all possible values for  , ,
but the only one that will make  and and  , so , so
 --> -->  --> -->  --> --> 
So Jane is  and John is and John is  , ,
The difference in their ages is, and always was  years. years.
Jane is 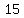 , John was , John was  . .
At that point Jane, always  years younger, was years younger, was  . .
In 3 years (3 years from toady), John will be  , ,
and that is four times as old as  years old. years old.
|
|
|