Question 669979: Greeting,
Would you please help me with this problem?
Explain how the order of operations determines how you evaluate an algebraic expression. Be sure to explain the rules for addition, subtraction, multiplication, division, and the use of grouping symbols. Use examples to illustrate your points.
Thanks a lot,
H.H
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! A DETAILED ANSWER:
Grouping symbols (parenthesis and the like) have priority
(25+35)/(3x5)=60/15=4 (I'm using x for multiplication)
because 25+35=60 and 3*5=15 must be calculated first.
Note that grouping symbols may not appear as parentheses.
For example, 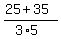 =(25+35)/(3x5) =(25+35)/(3x5)
because that long horizontal fraction bar (no need to memorize a name for it)
groups what's on top of the line as one group,
and what's below the line as another group.
Radicals are also grouping symbols,
as in 
Multiplication and division have equal standing and if several multiplications and divisions are in a row, they are done from left to right, as written.
(I'll be using x for multiplication, and / for division).
So 6x10/5/3x2=60/5/3x2=12/3x2=4x2=8
However, multiplication and division have priority over addition and subtraction.
So 5x3+7x2-12/4=15+14-3=26
Addition and subtraction (done last) have equal standing, and if several additions and subtractions are in a row, they are done from left to right, as written.
So 5-3+2-1+7=2+2-1+7=4-1+7=3+7=10
MORE:
Things can get complicated.
When faced with a complicated expression, we look for grouping symbols, and calculate the groups first.
In calculating each groups we follow order of operations to
Inside groups, or when all grouping symbols groups are calculated,
we look for plus and minus signs (to be done last),
and calculate the strings of divisions and multiplications in between the plus and minus signs first.
In a complicated example like (6x(10/5)+3x2)x5/(3-2)+3x2-20/5+3,
I see it as addition/subtraction involving four packages:
the complicated (6x(10/5)+3x2)x5/(3-2) first term,
+3x2, -1/5, and +3
The packages (terms) need to be calculated first.
The first package, (6x(10/5)+3x2)x5/(3-2) has lots of parentheses.
I have to start from the ones that do not have another set of parentheses inside.
So I calculate 3-2=1, and 10/5=2 first and write
(6x2+3x2)x5/1 in place of (6x(10/5)+3x2)x5/(3-2).
So far I have:
(6x(10/5)+3x2)x5/(3-2)+3x2-20/5+3=
(6x2+3x2)x5/1+3x2-20/5+3
Now, I have to calculate 6x2+3x2 because it is in parentheses,
but that expression has multiplication and addition.
I calculate first the products (6x2=12 and 3x2=6) that are separated by the plus sign.
After that I add the products (12+6=18) and I'm free from parentheses.
(6x(10/5)+3x2)x5/(3-2)+3x2-20/5+3=
(6x2+3x2)x5/1+3x2-20/5+3=
(12+6)x5/1+3x2-20/5+3=
18x5/1+3x2-20/5+3
Now I have do any calculations needed inside the four packages (terms) that are separated by the plus and minus signs.
Since 18x5/1=90/1=90, 3x2=6, and 20/5=4,
18x5/1+3x2-1/5+3=90+6-4+3,
so that is the next thing that's written, and the rest, is easy.
The whole thing is:
(6x(10/5)+3x2)x5/(3-2)+3x2-20/5+3=
(6x2+3x2)x5/1+3x2-20/5+3=
(12+6)x5/1+3x2-20/5+3=
18x5/1+3x2-20/5+3=
90+6-4+3=95
|
|
|